 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1984 >> Районный тур >> 9 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1984. Районный тур. 9 класс |
|
|
Решение: После перенесения всех слагаемых в левую часть и домножения на 2 получим:
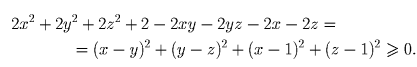
Задача 2: Задача 3: Решить уравнение:
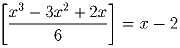
Решение: Левая часть уравнения – целое число, значит, x – целое число. Тогда x³ – 3x² + 2x = x(x – 1)(x – 2) делится на 6 и, следовательно,
 . Это уравнение имеет корни
x = 2, x = 3 или x = – 2.
Задача 4:
Дана замкнутая ломанная A1A2A3 … A10; точки B1,B2, … ,B10 –
середины ее звеньев, занумерованные в произвольном порядке.
Докажите, что
. Это уравнение имеет корни
x = 2, x = 3 или x = – 2.
Задача 4:
Дана замкнутая ломанная A1A2A3 … A10; точки B1,B2, … ,B10 –
середины ее звеньев, занумерованные в произвольном порядке.
Докажите, что 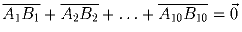 .
.Решение: Заметим, что каждый вектор
 можно представить в виде
разности
можно представить в виде
разности  , где O – какая-то точка плоскости.
Тогда
, где O – какая-то точка плоскости.
Тогда

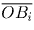 равна сумме векторов
OAi.
Вектор,
проведенный из точки O в середину отрезка AkAn, равен полусумме
векторов
равна сумме векторов
OAi.
Вектор,
проведенный из точки O в середину отрезка AkAn, равен полусумме
векторов 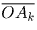 и
и 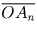 . Значит, сумма
. Значит, сумма  равна сумме
полусумм векторов
равна сумме
полусумм векторов  ,
, 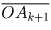 , k = 1,2, … 10 (считаем A11 = A1).
Каждый вектор
, k = 1,2, … 10 (считаем A11 = A1).
Каждый вектор  входит ровно в две такие полусуммы. Значит,
входит ровно в две такие полусуммы. Значит,
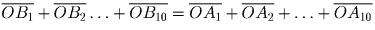 , что и требовалось доказать.
Задача 5:
ABCDA1B1C1D1 – куб с ребром 1м. На ребрах AA1,AB,CD выбраны
соответственно точки K, L, M так, что AK = 95см., AL = 70см.,
CM = 26см. Пересекает ли плоскость KLM ребро C1D1?
, что и требовалось доказать.
Задача 5:
ABCDA1B1C1D1 – куб с ребром 1м. На ребрах AA1,AB,CD выбраны
соответственно точки K, L, M так, что AK = 95см., AL = 70см.,
CM = 26см. Пересекает ли плоскость KLM ребро C1D1?Решение: AK = 95 см., AL = 70 см., CM = 26 см. Будем строить наше сечение:
X – точка пересечения ML и AD. 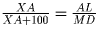 , тогда XA = 1750 см;
, тогда XA = 1750 см;
Y – точка пересечения XK и A1D1; 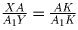 , тогда
, тогда 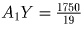 см;
см;
Z – точка пересечения LK и B1A1;  , тогда
, тогда 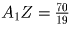 см;
см;
О – точка пересечения ZY и C1D1; 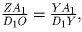 тогда
тогда 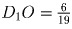 см < 100 см, то есть O лежит на отрезке
C1D1. Значит сечение пересекает ребро C1D1.
см < 100 см, то есть O лежит на отрезке
C1D1. Значит сечение пересекает ребро C1D1.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1984 >> Районный тур >> 9 класс | Убрать решения |