 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1985 >> Районный тур >> 10 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1985. Районный тур. 10 класс |
|
|
Решение: Пусть l – длина боковых ребер; a,b,c – стороны основания, α , β , γ – противолежащие им плоские углы при вершине D. Чтобы доказать, что треугольник ABC остроугольный, достаточно проверить, что квадрат любой из его сторон меньше суммы квадратов двух других его сторон. Проверим, например, что a² < b² + c²: a² = 2l²(1 – cos α );b² + c² = 2l²(1 – cos β ) + 2l²(1 – cos γ ) – по теореме косинусов. Доказываемое неравенство принимает вид 1 – cos α < 2 – cos β – cos γ – верно для тупых углов α , β , γ , так как 1 – cos α < 2 < 2 – cos β cos γ . Задача 2: При каких целых a уравнение x4 – (a + 4)x² + (2a + 3) = 0 имеет целый корень?
Решение: Для того, чтобы биквадратное уравнение имело целый корень, необходимо, чтобы его дискриминант являлся точным квадратом. Дискриминант равен (a + 4)² – 4(2a + 3) = a² + 4 – точный квадрат лишь при a = 0. Тогда уравнение принимает вид x4 – 4x² + 3 = 0 и имеет целый корень x = 1. Задача 3:
Задача 4: Докажите, что
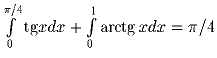 .
.Решение:
Заметим, что первый интеграл равен площади фигуры 1, а второй
интеграл равен площади фигуры 2 (см. рисунок). Сумма этих площадей
равна площади прямоугольника, то есть 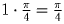 .
.
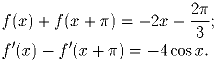
Решение: Продифференцировав первое равенство, получим систему

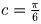 .
Значит,
.
Значит,  .
.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1985 >> Районный тур >> 10 класс | Убрать решения |