Задача 1:
Диагональные сечения правильной 8-угольной пирамиды,
проведенные через наибольшую и наименьшую диагонали основания,
равновелики. Под каким углом к основанию наклонена плоскость,
проходящая через вершину пирамиды и наименьшую диагональ
основания?
Решение:
Пусть H, h – высоты сечений, проведённых через
наибольшую и наименьшую диагонали основания; S, s – их площади;
R – радиус окружности, описанной около основания. Заметим, что
длины наибольшей и наименьшей диагоналей 2R и
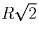
,
соответственно. Высота сечения, проведенного через наименьшую
диагональ
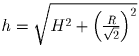
. Вычислим
площади сечений: S = ½ • 2R • H,
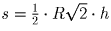
. Так как S = s, то
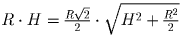
, откуда
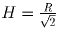
, и h = R. Синус искомого угла равен
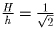
, то есть искомый угол равен 45
.
Задача 2:
Найти уравнение прямой, касающейся графика функции
y = x
4 – 2x³ + x² + x – 2
в двух точках.
Решение:
36. Аналогично задаче 31.
Задача 3:
Задача 4:
Докажите, что
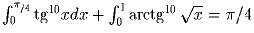
.
Решение:
Аналогично задаче 31.
Аналогично задаче 31.
Задача 5:


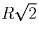 ,
соответственно. Высота сечения, проведенного через наименьшую
диагональ
,
соответственно. Высота сечения, проведенного через наименьшую
диагональ 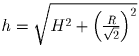 . Вычислим
площади сечений: S = ½ • 2R • H,
. Вычислим
площади сечений: S = ½ • 2R • H, 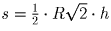 . Так как S = s, то
. Так как S = s, то 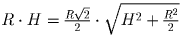 , откуда
, откуда 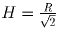 , и h = R. Синус искомого угла равен
, и h = R. Синус искомого угла равен 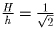 , то есть искомый угол равен 45 .
Задача 2:
Найти уравнение прямой, касающейся графика функции
y = x4 – 2x³ + x² + x – 2
в двух точках.
, то есть искомый угол равен 45 .
Задача 2:
Найти уравнение прямой, касающейся графика функции
y = x4 – 2x³ + x² + x – 2
в двух точках.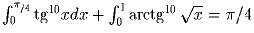 .
.