Задача 1:
Задача 2:
17 пионеров нашли 180 грибов, причем никакие двое не нашли
одинакового количества грибов. Докажите, что у какого-то пионера
число грибов делилось на 5.
Решение:
Предположим, что ни у одного из пионеров число грибов не кратно
пяти. Тогда общее количество собранных грибов не меньше, чем
сумма 1 + 2 + 3 + 4 + 6 + … + 19 + 21 + 22 (в сумму входят 17 первых не
делящихся на 5 натуральных чисел), которая равна

, что противоречит
условию. Значит, предположение неверно.
Задача 3:
Пионеры ходили на далёкое озеро, до которого 12км. Часть пути
они шли в гору со скоростью 3 км/ч, часть – по ровному месту со
скоростью 4 км/ч, а часть – под гору со скоростью 5 км/ч. Дорога
туда и обратно заняла 6 ч 16 мин. Сколько времени пионеры шли по
ровному месту?
Решение:
Пусть x – время, затраченное на весь путь по ровному месту.
Тогда

– длина ровного пути, а

–
общая длина
остального пути. За путь «туда и обратно» пионеры один раз
пройдут это расстояние, идя в гору, а другой раз – спускаясь с
горы. Значит общее время, затраченное на прогулку
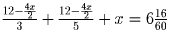
. Откуда x = 2 (часа).
Задача 4:
M и N – середины сторон BC и CD квадрата ABCD.
Отрезки BN и DM
пересекаются в точке O. Докажите, что прямая AO является
биссектрисой угла BAD.
Решение:
Рассмотрим симметрию относительно AC. При этом точка C
останется на месте, а точки B и D перейдут друг в друга.
Тогда перейдут друг в друга точки M и N, а, значит,
точка пересечения отрезков BN и DM перейдет сама в себя,
а это и означает, что она лежит на AC – биссектрисе угла BAD.


 , что противоречит
условию. Значит, предположение неверно.
Задача 3:
Пионеры ходили на далёкое озеро, до которого 12км. Часть пути
они шли в гору со скоростью 3 км/ч, часть – по ровному месту со
скоростью 4 км/ч, а часть – под гору со скоростью 5 км/ч. Дорога
туда и обратно заняла 6 ч 16 мин. Сколько времени пионеры шли по
ровному месту?
, что противоречит
условию. Значит, предположение неверно.
Задача 3:
Пионеры ходили на далёкое озеро, до которого 12км. Часть пути
они шли в гору со скоростью 3 км/ч, часть – по ровному месту со
скоростью 4 км/ч, а часть – под гору со скоростью 5 км/ч. Дорога
туда и обратно заняла 6 ч 16 мин. Сколько времени пионеры шли по
ровному месту? – длина ровного пути, а
– длина ровного пути, а  –
общая длина
остального пути. За путь «туда и обратно» пионеры один раз
пройдут это расстояние, идя в гору, а другой раз – спускаясь с
горы. Значит общее время, затраченное на прогулку
–
общая длина
остального пути. За путь «туда и обратно» пионеры один раз
пройдут это расстояние, идя в гору, а другой раз – спускаясь с
горы. Значит общее время, затраченное на прогулку
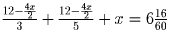 . Откуда x = 2 (часа).
Задача 4:
M и N – середины сторон BC и CD квадрата ABCD.
Отрезки BN и DM
пересекаются в точке O. Докажите, что прямая AO является
биссектрисой угла BAD.
. Откуда x = 2 (часа).
Задача 4:
M и N – середины сторон BC и CD квадрата ABCD.
Отрезки BN и DM
пересекаются в точке O. Докажите, что прямая AO является
биссектрисой угла BAD.