Задача 1:
Про положительные числа a, b, c известно, что
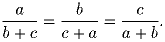
Докажите, что
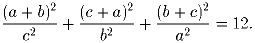
Решение:
Прибавив к каждой части данного равенства по единице, получим
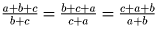
. Так как
числа положительные, то b + c = c + a = a + b и, следовательно,
a = b = c. Откуда и получаем требуемое.
Задача 2:
Из каждой вершины 4-угольника провели векторы к серединам всех
его сторон. Докажите, что сумма шестнадцати образовавшихся
векторов равна
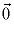
.
Решение:
Пусть K, L, M, N – середины сторон AB, BC, CD,
DA
соответственно. Сумма векторов лежащих на сторонах
четырехугольника равна
. Также и
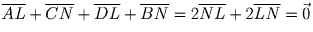
.
Аналогично, равна нулю сумма оставшихся четырех векторов. Что и
требовалось.
Задача 3:
Докажите, что дробь
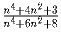
несократима ни при каких
целых n.
Решение:
Пусть числитель и знаменатель имеют общий делитель k > 1,
то есть
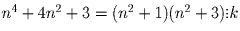
и
n
4 + 6n² + 8 = (n² + 4)(n² + 2) делится на k.
Оба сомножителя числителя взаимно просты с n² + 2.
Значит, из того, что
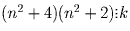
, следует, что
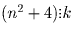
. Так как n² + 4 взаимно просто
с n² + 3, то из того, что

,
следует, что
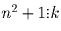
. Поскольку
n² + 4 и n² + 1 делятся на k, то

. Тогда
k должно равняться 3, чего быть не может, так как n² не может
давать остаток 2 при делении
на 3. Значит, предположение неверно и дробь
несократима.
Задача 4:
На стороне AB треугольника ABC взяли точку M такую, что
AM = ⅓AB. В каком отношении отрезок CM делит медиану,
проведенную из вершины A?
Решение:
Проведем медианы CC
1 и AA
1 треугольника ABC.
Пусть K – точка
их пересечения, O – точка пересечения MC и AA
1. Заметим, что
C
1M = ⅓C
1A и C
1K = ⅓C
1C.
Значит, MK || AC и треугольники MOK и COA
подобны. Отсюда заключаем, что

и, следовательно,
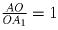
, то есть CM делит отрезок AA
1 пополам.
Задача 5:


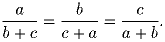
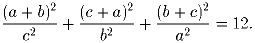
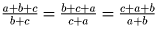 . Так как
числа положительные, то b + c = c + a = a + b и, следовательно,
a = b = c. Откуда и получаем требуемое.
Задача 2:
Из каждой вершины 4-угольника провели векторы к серединам всех
его сторон. Докажите, что сумма шестнадцати образовавшихся
векторов равна
. Так как
числа положительные, то b + c = c + a = a + b и, следовательно,
a = b = c. Откуда и получаем требуемое.
Задача 2:
Из каждой вершины 4-угольника провели векторы к серединам всех
его сторон. Докажите, что сумма шестнадцати образовавшихся
векторов равна 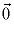 .
.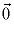 . Также и
. Также и 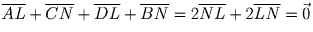 .
Аналогично, равна нулю сумма оставшихся четырех векторов. Что и
требовалось.
Задача 3:
Докажите, что дробь
.
Аналогично, равна нулю сумма оставшихся четырех векторов. Что и
требовалось.
Задача 3:
Докажите, что дробь 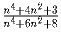 несократима ни при каких
целых n.
несократима ни при каких
целых n.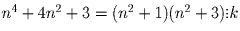 и
n4 + 6n² + 8 = (n² + 4)(n² + 2) делится на k.
Оба сомножителя числителя взаимно просты с n² + 2.
Значит, из того, что
и
n4 + 6n² + 8 = (n² + 4)(n² + 2) делится на k.
Оба сомножителя числителя взаимно просты с n² + 2.
Значит, из того, что 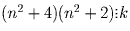 , следует, что
, следует, что
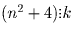 . Так как n² + 4 взаимно просто
с n² + 3, то из того, что
. Так как n² + 4 взаимно просто
с n² + 3, то из того, что  ,
следует, что
,
следует, что 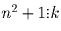 . Поскольку
n² + 4 и n² + 1 делятся на k, то
. Поскольку
n² + 4 и n² + 1 делятся на k, то  . Тогда
k должно равняться 3, чего быть не может, так как n² не может
давать остаток 2 при делении
на 3. Значит, предположение неверно и дробь
несократима.
Задача 4:
На стороне AB треугольника ABC взяли точку M такую, что
AM = ⅓AB. В каком отношении отрезок CM делит медиану,
проведенную из вершины A?
. Тогда
k должно равняться 3, чего быть не может, так как n² не может
давать остаток 2 при делении
на 3. Значит, предположение неверно и дробь
несократима.
Задача 4:
На стороне AB треугольника ABC взяли точку M такую, что
AM = ⅓AB. В каком отношении отрезок CM делит медиану,
проведенную из вершины A? и, следовательно,
и, следовательно,
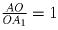 , то есть CM делит отрезок AA1 пополам.
Задача 5:
, то есть CM делит отрезок AA1 пополам.
Задача 5: