Задача 1:
Функция y = f(x) определена при всех вещественных значениях
переменной, и при всех x выполнено равенство 2 • f(x) + f(1 – x) = 3x².
Найдите f(5).
Решение:
Запишем данное равенство для x = k и x = 1 – k:
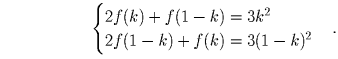
Решая систему, находим, что f(k) = k² + 2k – 1;
f(5) = 34.
Задача 2:
M – середина медианы AD треугольника ABC, имеющего площадь S.
Прямая BM пересекает сторону AC в точке F. Найдите площадь
треугольника AMF.
Решение:
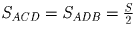
;

. Пусть S
AMF = x.
Тогда
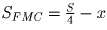
,
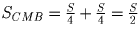
,
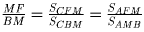
, откуда

и

– искомая площадь.
Задача 3:
Задача 4:
Две окружности пересекаются в точках A и B; M и N – точки,
диаметрально противоположные A в первой и второй окружностях. К
окружностям проведены касательные в точке A. Касательная к
первой пересекает вторую в точке C, а касательная ко второй
пересекает первую в точке D. Докажите, что треугольники ACM и
ADN равновелики.
Решение:
Треугольники AMD и ANC подобны, так как
∠ MDA = ∠ ACN = 90
(как опирающиеся на
диаметры), ∠ MAD = ∠ CAN. Следовательно,
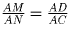
, откуда получаем, что

, а это и есть отношение площадей прямоугольных треугольников
MAC и DAN. Значит, эти треугольники равновелики.
Задача 5:
Решить в целых числах: (x + 1)(y² – x² – 4) = x².
Решение:
При x + 1 = 0 равенство невозможно. Значит
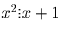
,
поскольку числа x и x + 1 взаимно просты, это возможно лишь при
x + 1 = ± 1. Отсюда находим решения уравнения: x = 0,y = 2; x = 0,y = – 2; x = – 2,y = 2; x = – 2,y = – 2.


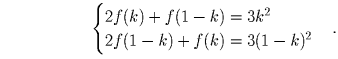
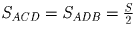 ;
;  . Пусть SAMF = x.
Тогда
. Пусть SAMF = x.
Тогда 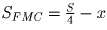 ,
, 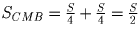 ,
,
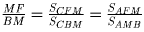 , откуда
, откуда  и
и
 – искомая площадь.
Задача 3:
– искомая площадь.
Задача 3: 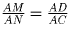 , откуда получаем, что
, откуда получаем, что  , а это и есть отношение площадей прямоугольных треугольников
MAC и DAN. Значит, эти треугольники равновелики.
Задача 5:
Решить в целых числах: (x + 1)(y² – x² – 4) = x².
, а это и есть отношение площадей прямоугольных треугольников
MAC и DAN. Значит, эти треугольники равновелики.
Задача 5:
Решить в целых числах: (x + 1)(y² – x² – 4) = x².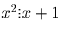 ,
поскольку числа x и x + 1 взаимно просты, это возможно лишь при
x + 1 = ± 1. Отсюда находим решения уравнения: x = 0,y = 2; x = 0,y = – 2; x = – 2,y = 2; x = – 2,y = – 2.
,
поскольку числа x и x + 1 взаимно просты, это возможно лишь при
x + 1 = ± 1. Отсюда находим решения уравнения: x = 0,y = 2; x = 0,y = – 2; x = – 2,y = 2; x = – 2,y = – 2.