Задача 1:
Что больше:
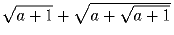
или
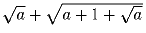
?
Решение:
После возведения в квадрат получим очевидное неравенство:

.
Значит, первое из выражений было больше.
Задача 2:
Задача 3:
Задача 4:
Сумму дробей
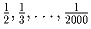
представили в виде
несократимой дроби. Сколькими нулями оканчивается ее
знаменатель?
Решение:
Наименьшее общее кратное знаменателей содержит двойку в 10-й
степени. При приведении дробей к наименьшему общему знаменателю,
числители всех дробей кроме

будут
домножаться на 2. Значит, получившаяся в числителе сумма будет
нечетна, то есть знаменатель нашей несократимой дроби будет
содержать 2¹º. Выясним, какая в нем будет степень пяти. Все
дроби, кроме
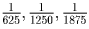
будут
домножаться на 5, 25 или 125, а эти три дроби домножатся на числа
3A, 2A, A соответственно (A не кратно пяти). Таким образом
в числителе окажется сумма вида 5X + 3A + 2A + A = 5X + 6A, которая не
делится на 5. Значит, знаменатель нашей несократимой дроби будет
содержать 5
4. Таким образом, знаменатель оканчивается на четыре
нуля.
Задача 5:


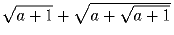 или
или 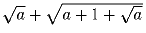 ?
? .
Значит, первое из выражений было больше.
Задача 2:
.
Значит, первое из выражений было больше.
Задача 2: 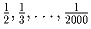 представили в виде
несократимой дроби. Сколькими нулями оканчивается ее
знаменатель?
представили в виде
несократимой дроби. Сколькими нулями оканчивается ее
знаменатель? будут
домножаться на 2. Значит, получившаяся в числителе сумма будет
нечетна, то есть знаменатель нашей несократимой дроби будет
содержать 2¹º. Выясним, какая в нем будет степень пяти. Все
дроби, кроме
будут
домножаться на 2. Значит, получившаяся в числителе сумма будет
нечетна, то есть знаменатель нашей несократимой дроби будет
содержать 2¹º. Выясним, какая в нем будет степень пяти. Все
дроби, кроме 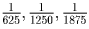 будут
домножаться на 5, 25 или 125, а эти три дроби домножатся на числа
3A, 2A, A соответственно (A не кратно пяти). Таким образом
в числителе окажется сумма вида 5X + 3A + 2A + A = 5X + 6A, которая не
делится на 5. Значит, знаменатель нашей несократимой дроби будет
содержать 54. Таким образом, знаменатель оканчивается на четыре
нуля.
Задача 5:
будут
домножаться на 5, 25 или 125, а эти три дроби домножатся на числа
3A, 2A, A соответственно (A не кратно пяти). Таким образом
в числителе окажется сумма вида 5X + 3A + 2A + A = 5X + 6A, которая не
делится на 5. Значит, знаменатель нашей несократимой дроби будет
содержать 54. Таким образом, знаменатель оканчивается на четыре
нуля.
Задача 5: