Задача 1:
Вычислите:
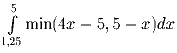
.
Решение:
Построим график подинтегральной функции и
заметим, что искомый интеграл равен площади заштрихованного
треугольника, то есть S = ½ • 3(5 – 1¼) = 5⅝.
Задача 2:
Задача 3:
Задача 4:
M – произвольная точка основания ABC тетраэдра ABCD. Через
точку M проведены сечения параллельные боковым граням. Пусть S
1,
S
2 и S
3 – площади боковых граней; x, y, z – площади
соответствующих сечений. Докажите, что
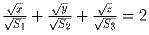
.
Решение:
Пусть A
1C
P – сечение, параллельное ACD,
A
1 ∈ AB, C
1 ∈ CB. Треугольники ACD и A
1C
1P
подобны, значит, их площади относятся как квадраты соответствующих
длин. Пусть b′ – длина A
1C
1; b – длина AC. Тогда

. Определим
аналогично длины a, a′, c, c′. Тогда доказываемое
равенство примет вид
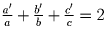
.
Проверим это. Продолжим отрезок BM и обозначим K
точку пересечения AC и BM.
Заметим, что
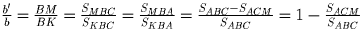
. Записав
аналогичные равенства для

и
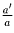
,
получим, что
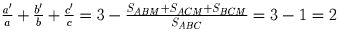
, что и требовалось.
Задача 5:


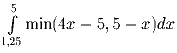 .
.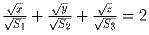 .
. . Определим
аналогично длины a, a′, c, c′. Тогда доказываемое
равенство примет вид
. Определим
аналогично длины a, a′, c, c′. Тогда доказываемое
равенство примет вид 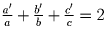 .
Проверим это. Продолжим отрезок BM и обозначим K
точку пересечения AC и BM.
Заметим, что
.
Проверим это. Продолжим отрезок BM и обозначим K
точку пересечения AC и BM.
Заметим, что 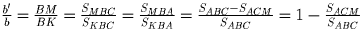 . Записав
аналогичные равенства для
. Записав
аналогичные равенства для  и
и 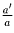 ,
получим, что
,
получим, что
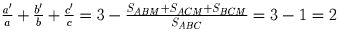 , что и требовалось.
Задача 5:
, что и требовалось.
Задача 5: