Задача 1: Решить систему уравнений:

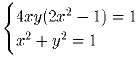
Решение: Отметим, что |x|,|y| ≤ 1. Сделаем подстановку x =  cos  α , y =  sin  α . Тогда первое уравнение примет вид  sin 4 α  = 1, откуда , k – целое число. Тогда решение нашего уравнения имеет вид 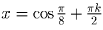, 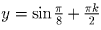Воспользовавшись формулами синуса и косинуса половинных углов, выразим решения в радикалах.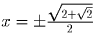

; или (Надо брать только верхние или только нижние знаки).

Задача 2: На ребрах произвольного тетраэдра указали направления. Может ли сумма полученных таким образом шести векторов оказаться равной нуль-вектору?

Решение: Проведем высоту тетраэдра и рассмотрим проекции векторов на эту прямую. Проекции векторов основания равны нулю, а проекции трех оставшихся векторов равны по длине и, следовательно, их сумма отлична от 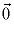, таким образом сумма проекций всех векторов на эту прямую отлично от 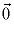. Значит сумма наших векторов не может быть равна .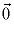

Задача 3: Функция f задана на всей вещественной оси, причем для любого x имеет место равенство: f(x + 1)f(x) + f(x + 1) + 1 = 0. Доказать, что f не может быть непрерывной.

Решение: Перепишем условия в виде f(x + 1)(1 + f(x)) =  – 1 и заметим, что f(x) не принимает значений 0 и  – 1. Тогда, если f непрерывна, то все е. значения лежат только в одном из промежутков ( –  ∞ , – 1); ( – 1,0); (0, +  ∞ ). Рассмотрим первый случай: если f(x) <  – 1 при любом x, то f(x + 1)(1 + f(x)) > 0 – противоречит условию. Аналогично рассматриваем два других случая – они также противоречат условию. Значит, f не непрерывна.

Задача 4: Найдите вещественные числа a, b, c, d, если известно, что

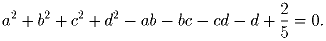
Решение: Перепишем данное равенство в виде

откуда d = 4/5, c = 3/5, b = 2/5, a = 1/5.

Задача 5: AM, BN, CP – высоты остроугольного треугольника ABC. Доказать, что MN • NP • MP = AN • BP • CM.

Решение: Пусть O – точка пересечения высот. Четырёхугольники OMCN и PNCB – вписанные, значит  ∠ OMN =  ∠ OCN =  ∠ PBN. Аналогично проверяется, что  ∠ MNO =  ∠ BNP. Тогда треугольники MNO и BNP подобны. Значит, 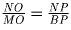. Умножив это равенство на два аналогичных, получим 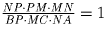. Что и требовалось.