Задача 1: Может ли сумма цифр трамвайного билета делиться и на 5, и на 11?

Решение: Не может. Самое маленькое натуральное число, делящееся на 5 и на 11 – число 55. Но самая большая сумма цифр трамвайного билета всего 6 • 9 = 54.

Задача 2: Расставьте в вершинах треугольника и в серединах его сторон числа 1, 2, 3, 4, 5, 6 так, чтобы сумма любых трех, расставленных вдоль одной стороны, была одной и той же и возможно меньшей.

Решение: Пусть x – сумма чисел вдоль стороны; a,b,c – числа, стоящие в углах. Тогда 3x = 1 + 2 + 3 + 4 + 5 + 6 + a + b + c, то есть 3x = 21 + a + b + c, так как a + b + c ≥ 1 + 2 + 3 = 6, то x ≥ 9 – минимальная сумма цифр на стороне. Достигается при такой расстановке:

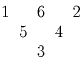
Задача 3: Сколько на шахматной доске имеется всевозможных прямоугольников, состоящих из четырех клеток?

Решение: Четырехугольник, состоящий из 4-х клеток, может иметь размеры 1 × 4 или 2 × 2. Любая клетка, кроме клеток самого верхнего и самого правого рядов, может быть левым нижним углом квадрата 2 × 2, поэтому таких квадратов будет 7 • 7 = 49 штук. Прямоугольники 1 × 4 могут быть расположены горизонтально или вертикально. И тех и других будет по 5 • 8 = 40 штук. Значит, всего прямоугольников 129 штук.

Задача 4: В автопарке было несколько пятитонных грузовиков и несколько трёхтонных. Чтобы вывезти некоторый груз, требуется загрузить все пятитонные грузовики и один трёхтонный или все трёхтонные и два пятитонных. Сколько и каких грузовиков было, если их общая грузоподъёмность меньше 50 тонн.

Решение: Пусть a – количество пятитонных, b – количество трёхтонных грузовиков. Тогда 5a + 3 = 3b + 10 и 5a + 3b ≤ 50. Выразим 3b из уравнения и подставим в неравенство: 5a + (5a – 7) = 10a – 7 ≤ 50. Таким образом a может принимать значения 0, 1, 2, 3, 4, 5. Целые значения b получаем лишь при a = 2 (b = 1) и a = 5 (b = 6). То есть возможное количество пятитонных и трёхтонных грузовиков: 2 и 1 или 5 и 6 соответственно.