Задача 1:
Задача 2:
Вычислите значение выражения:
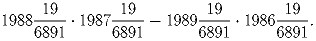
Решение:
Пусть

.
Тогда выражение примет вид
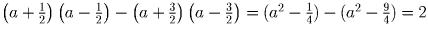
.
Задача 3:
В трапеции ABCD (AD – основание) AB = BC, AC = CD, BC + CD = AD.
Найдите углы трапеции.
Решение:
Возьмём на AD точку M такую, что AM = BC и обозначим
α = ∠ BCA. Тогда, учитывая, что ABCM – ромб, нетрудно
видеть, что ∠ BAC = ∠ CAD = ∠ ACM = ∠ CDA = α .
Кроме того ∠ CMD = 2 α (как внешний угол треугольника
ACM), ∠ MCD = 2 α (так как MD = AD – BC = CD). Поэтому в
треугольнике MCD сумма углов равна 5 α , откуда
α = 36
. Теперь легко найти и углы трапеции: 72
, 108
, 144
, 36°.
Задача 4:
Что больше: сумма всех цифр всех четырехзначных чисел или
сумма всех цифр всех делящихся на 9 пятизначных чисел?
Решение:
К каждому четырехзначному числу можно приписать справа
цифру так, что получится пятизначное число, делящееся на 9.
Значит сумма всех цифр всех пятизначных чисел, делящихся на 9,
содержит сумму всех цифр всех четырехзначных чисел и,
следовательно, она больше.


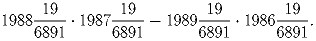
 .
Тогда выражение примет вид
.
Тогда выражение примет вид 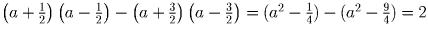 .
Задача 3:
В трапеции ABCD (AD – основание) AB = BC, AC = CD, BC + CD = AD.
Найдите углы трапеции.
.
Задача 3:
В трапеции ABCD (AD – основание) AB = BC, AC = CD, BC + CD = AD.
Найдите углы трапеции.