 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1986 >> Районный тур >> 8 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1986. Районный тур. 8 класс |
|
|
Задача 2:
Задача 3: Решите уравнение: max (x² – x + 1,4x – x²) = 3.
Решение:
Равенство max (x² – x + 1,4x – x²) = 3 означает, что одно из чисел x² – x + 1 и 4x – x² равно трём, а другое не превосходит трёх. Если x² – x + 1 = 3, то x = 2 или x = – 1. Если 4x – x² = 3, то x = 3 или x = 1. В каждом случае осталось проверить, что другое число меньше трёх. Это верно только при x = 1 и x = – 1. Значит исходное уравнение имеет два корня x = ± 1.
Задача 4: H – середина стороны CD параллелограмма ABCD. Отрезок BH пересекает диагональ AC в точке K, а отрезок AH пересекает диагональ BD в точке M. Докажите, что точки K и M делят отрезок прямой KM, заключенный между сторонами BC и AD, на три равные части.Решение:
Пары треугольников ABM, HDM и ABK, CHK подобны с
коэффициентом ½. Значит  и
прямые KM и CD параллельны. Пусть
X и Y – точки пересечения KM со сторонами BC и AD
соответственно. Рассматривая пары подобных треугольников ABC и
KXC, ABD и YMD, находим, что KX = ⅓AB, MY = ⅓AB,
что и даёт нам требуемое.
и
прямые KM и CD параллельны. Пусть
X и Y – точки пересечения KM со сторонами BC и AD
соответственно. Рассматривая пары подобных треугольников ABC и
KXC, ABD и YMD, находим, что KX = ⅓AB, MY = ⅓AB,
что и даёт нам требуемое.
Решение: Если
 , то
, то  ,
то есть
,
то есть  , и, значит,
, и, значит, 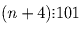 ,
откуда n = 101k – 4, k – целое. Так как n – трехзначное число,
то k может принимать целые значения от 2 до 9.
,
откуда n = 101k – 4, k – целое. Так как n – трехзначное число,
то k может принимать целые значения от 2 до 9.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1986 >> Районный тур >> 8 класс | Убрать решения |