Задача 1: В прямой угол C вписана окружность (M и N – точки касания).Через произвольную точку K меньшей дуги MN проведена касательная к окружности, пересекающая стороны угла в точках A и B. Докажите, что произведение (AB + AC)(AB + BC) постоянно и не зависит от выбора точки K на дуге.

Решение: Пусть R – радиус окружности;  α ,  β  – углы BOK и AOK соответственно (O – центр окружности). Тогда MC = NC = R; BM = BK = R tg  β ; NA = AK = R tg  α ;

(в последнем переходе мы воспользовались тем, что  α  +  β  = 45  , то есть  tg ( α  +  β ) = 1 и )

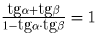Задача 2: Дана функция: . Найти сумму:

Решение: Заметим, что 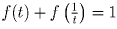. Значит, искомая сумма равна 1. Пусть R – радиус окружности;  α ,  β  – углы BOK и AOK соответственно (O – центр окружности). Тогда MC = NC = R;

BM = BK = R tg  β ; NA = AK = R tg  α ; (AB + AC)(AB + BC) = (R tg  α  + R tg  β  + R – R tg  α )(R tg  α  + R tg  β  + R – R tg  β ) = R²( tg  β  + 1)(1 +  tg  α ) = R²(1 +  tg  α  +  tg  β  +  tg  α  •  tg  β ) = 2R² (в последнем переходе мы воспользовались тем, что  α  +  β  = 45  , то есть  tg ( α  +  β ) = 1 и ) .

Задача 3: Из произвольной точки D на гипотенузе AB прямоугольного треугольника ABC опущены перпендикуляры DK и DM на катеты треугольника. При каком выборе точки D на гипотенузе площадь треугольника DKM будет наибольшей?

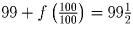Решение: 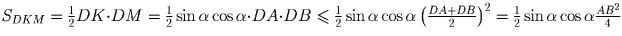( α  – острый угол треугольника ABC). Таким образом наибольшая площадь треугольника DKM равна 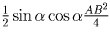, что достигается при DA = DB, то есть когда точка D является серединой гипотенузы.

Задача 4: Докажите, что система уравнений имеет единственное вещественное решение x = y = z = 0.

Решение: Пусть x ≤ y ≤ z. Тогда x + 2x³ ≤ y + 2y³ ≤ z + 2z³ и, значит, z³ ≤ x³ ≤ y³, откуда получаем, что все три числа x, y и z равны. Теперь, решив уравнение x³ = x + 2x³, получаем, что x = y = z = 0.

Задача 5: