Задача 1:

Задача 2: На сторонах произвольного треугольника ABC произвольным образом выбраны точки M, N и P. Через M₁, N₁ и P₁ обозначены точки, симметричные точкам M, N и P относительно середин этих сторон. Докажите, что треугольники MNP и M₁N₁P₁ равновелики.

Решение: Обозначим S_ABC = S; 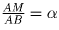; ; . Тогда 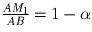; ; ; 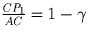S_CPN =  γ (1 –  β )S; S_NMB =  β (1 –  α )S; S_PMA =  α (1 –  γ )S.

Теперь выразим площадь треугольников PMN и P₁M₁N₁

Оба эти выражения равны (1 –  α  –  β  –  γ  +  α  β  +  α  γ  +  β  γ )S.

Задача 3: Множество A, состоящее из вещественных чисел, обладает следующим свойством: вместе с числом x оно содержит число 2x² – 1. Может ли A содержать ровно 100 чисел?

Решение: Пусть , k = 0,1,2, … ,99. Для этих чисел, во-первых, x_k ≠ x_m при k ≠ m. Во-вторых, для любого m ≥ 1 и 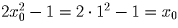. То есть наше множество x_k (k = 0, … ,99) обладает требуемыми свойствами.

Задача 4: Биссектрисы AA₁ и BB₁ треугольника ABC пересекаются в точке O. Докажите, что если угол C треугольника равен 60  , то OA₁ = OB₁.

Решение: 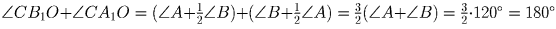. Значит, CB₁OA₁ – вписанный четырехугольник. Хорды B₁O и A₁O стягивают равные дуги (так как CO тоже биссектриса) и, следовательно, равны.

Задача 5: Дана невозрастающая последовательность неотрицательных чисел a₁ ≥ a₂ ≥  …  ≥ a_2n + 1 ≥ 0. Докажите неравенство:

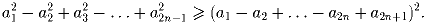
Решение: Проведем доказательство индукцией по n. При n = 0 неравенство очевидно. Пусть оно выполнено при n = k, то есть 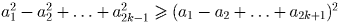. Чтобы получить неравенство для n = k + 1 достаточно проверить, что 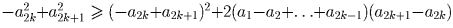(тогда, сложив это неравенство с неравенством для n = k, получим требуемое)

Преобразуем это неравенство: (a_2k – a_2k + 1)(a_2k + 1 – a_2k – a_2k – a_2k + 1 + 2a₁ – 2a₂ +  …  + 2a_2k – 1) ≥ 0, и (a_2k – a_2k + 1)(2a₁ – 2a₂ +  …  + 2a_2k – 1 – 2a_2k) ≥ 0 – верно. Значит, индукционный переход совершен. Что и требовалось.