Задача 1:
Площадь прямоугольного треугольника равна 7, 5 см², а его
периметр равен 15 см. Найдите стороны треугольника.
Решение:
Пусть a, b – катеты треугольника. Известно, что

и
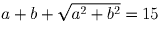
. Из второго
равенства заключаем, после возведения в квадрат, что a + b = 8,5.
Отсюда находим длины катетов: 6 и 2,5 и, значит, гипотенузы:
6,5.
Задача 2:
Докажите, что если
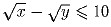
, то x – 2y ≤ 200.
Решение:
Возведём неравенство
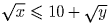
в квадрат:
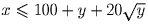
. Вычтем теперь 2y из обеих частей
неравенства и преобразуем выражение в правой части:

.
Задача 3:
Могут ли шесть попарных сумм четырех вещественных чисел
совпадать с числами 3, 4, 4, 5, 6, 8?
Решение:
Аналогично задаче 15.
Задача 4:
Вычислить
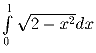
.
Решение:
Построим график подинтегральной функции и заметим, что
искомый интеграл равен сумме площадей заштрихованных
фигур.

.
Задача 5:
В треугольной пирамиде ABCD ребра AB,BC,CD попарно
перпендикулярны. Докажите, что шесть середин ребер пирамиды не
могут лежать на одной сфере.
Решение:
Пусть E, F, G, I, J и H – середины CD, DB,
DA, CB, AB и AC соответственно. FG и HI – средние
линии треугольников DAB и CAB, значит они параллельны и,
следовательно, лежат в одной плоскости, которая
перпендикулярна плоскости CDB. Центр любой сферы,
содержащей точки E, F и G, лежит на плоскости, проходящей через
середину EF перпендикулярно EF и, следовательно, параллельно
плоскости FGHI. Центр любой сферы, содержащей точки I, J и
H, лежит на плоскости, проходящей через середину HJ
перпендикулярно HJ и, значит, параллельно плоскости FGHI.
Плоскости, содержащие центры сфер, не имеют общих точек, поскольку
лежат по разные стороны от FGHI. Значит все шесть середин рёбер
тетраэдра ABCD не могут лежать на одной сфере.


 и
и 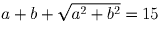 . Из второго
равенства заключаем, после возведения в квадрат, что a + b = 8,5.
Отсюда находим длины катетов: 6 и 2,5 и, значит, гипотенузы:
6,5.
Задача 2:
Докажите, что если
. Из второго
равенства заключаем, после возведения в квадрат, что a + b = 8,5.
Отсюда находим длины катетов: 6 и 2,5 и, значит, гипотенузы:
6,5.
Задача 2:
Докажите, что если 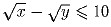 , то x – 2y ≤ 200.
, то x – 2y ≤ 200.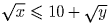 в квадрат:
в квадрат:
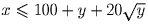 . Вычтем теперь 2y из обеих частей
неравенства и преобразуем выражение в правой части:
. Вычтем теперь 2y из обеих частей
неравенства и преобразуем выражение в правой части:  .
Задача 3:
Могут ли шесть попарных сумм четырех вещественных чисел
совпадать с числами 3, 4, 4, 5, 6, 8?
.
Задача 3:
Могут ли шесть попарных сумм четырех вещественных чисел
совпадать с числами 3, 4, 4, 5, 6, 8?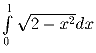 .
. .
.