 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1987 >> Районный тур >> 10 класс ФМШ | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1987. Районный тур. 10 класс ФМШ |
|
|
Решение: (1*a) • (a*1) = (1 • a)*(a • 1) = a*a = 1, то есть
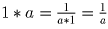 . Поэтому
. Поэтому 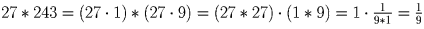 .
Замечание. Да и вообще
.
Замечание. Да и вообще
 .
Задача 2:
.
Задача 2: Задача 3: Вычислите:
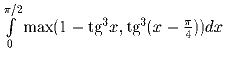 .
.Решение: Заметим, что 1 – tg³x ≥ tg³(x – π /4) при x ∈ (0; π /4) и наоборот при x ∈ ( π /4; π /2). Значит, наш интеграл равен:

Задача 4: На числовой оси задана трижды дифференцируемая функция f, для которой f(x) • f′(x) • f′′(x) = 0 в любой точке x. Докажите, что f – линейная функция.
Решение: Рассмотрим точку x, в которой f(x) не равно 0. Из непрерывности f следует, что существует окрестность точки x, в которой f(x) не равно 0. Тогда в этой окрестности f′ • f″ = 0, (f′²)′ = 0,
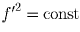 ,
, 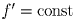 ,
f = ax + b – линейная функция. Таким образом, f линейна в
окрестности любой точки, в которой она не равна 0. Значит, f
кусочно линейна. Но, так как f дифференцируема, то она линейна на
всей числовой оси.
Задача 5:
Четыре сферы, центры которых не лежат в одной плоскости,
попарно пересекаются по окружностям. Докажите, что все шесть
плоскостей, в которых лежат окружности пересечений, пересекаются
в одной точке (центры никаких трех сфер не лежат на одной
прямой).
,
f = ax + b – линейная функция. Таким образом, f линейна в
окрестности любой точки, в которой она не равна 0. Значит, f
кусочно линейна. Но, так как f дифференцируема, то она линейна на
всей числовой оси.
Задача 5:
Четыре сферы, центры которых не лежат в одной плоскости,
попарно пересекаются по окружностям. Докажите, что все шесть
плоскостей, в которых лежат окружности пересечений, пересекаются
в одной точке (центры никаких трех сфер не лежат на одной
прямой).Решение: Рассмотрим сферы с центрами A и B, радиусами RA,RB и плоскость lAB, содержащую их пересечение. Для любой точки X из этой плоскости
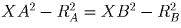 .
Действительно, если обозначить через Y точку пересечения
AB c lAB, то
.
Действительно, если обозначить через Y точку пересечения
AB c lAB, то
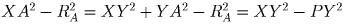 , где P –
точка пересечения сфер, лежащая в рассматриваемой плоскости.
Аналогично получаем, что
, где P –
точка пересечения сфер, лежащая в рассматриваемой плоскости.
Аналогично получаем, что 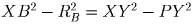 . Верно и
обратное: если
. Верно и
обратное: если 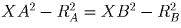 , то X лежит в
плоскости lAB. Рассмотрим теперь третью сферу (с центром C и
радиусом Rc). Так как A, B, C не лежат на одной прямой,
то плоскости lAB и lBC имеют общие точки, для которых
выполнено равенство
, то X лежит в
плоскости lAB. Рассмотрим теперь третью сферу (с центром C и
радиусом Rc). Так как A, B, C не лежат на одной прямой,
то плоскости lAB и lBC имеют общие точки, для которых
выполнено равенство
 и,
следовательно, X лежит в плоскости lAC. Так как все три
плоскости lAB, lAC, lBC перпендикулярны плоскости ABC
и пересекаются, то множество их пересечения – прямая l,
перпендикулярная плоскости ABC. Рассмотрим теперь плоскость
lAD, так как центры сфер не лежат в одной плоскости, то
lAD и l не параллельны и, следовательно, имеют ровно одну
общую точку O, для которой выполнено
и,
следовательно, X лежит в плоскости lAC. Так как все три
плоскости lAB, lAC, lBC перпендикулярны плоскости ABC
и пересекаются, то множество их пересечения – прямая l,
перпендикулярная плоскости ABC. Рассмотрим теперь плоскость
lAD, так как центры сфер не лежат в одной плоскости, то
lAD и l не параллельны и, следовательно, имеют ровно одну
общую точку O, для которой выполнено
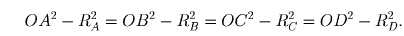
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1987 >> Районный тур >> 10 класс ФМШ | Убрать решения |