Задача 1: Пятеро октябрят – Паша, Даша, Саша, Маша и Наташа – построились в шеренгу, держа в руках 37 флажков. В каком порядке стоят ребята неизвестно. Октябрята, стоящие справа от Наташи, держат 14 флажков, справа от Саши – 32 флажка, справа от Паши – 20 флажков, справа от Маши – 8 флажков. Сколько флажков у каждого из ребят?

Решение: Чем левее стоит человек, тем больше флажков справа от него, значит октябрята стоят в таком порядке (слева направо): Саша, Паша, Наташа, Маша, Даша. У них 5, 12, 6, 6, 8 флажков соответственно.

Задача 2: Сумму двух натуральных чисел умножили на их произведение. Могло ли получиться 15015?

Решение: Нет, так как из чисел a, b, a + b хотя бы одно четное и, значит, четно их произведение.

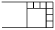
Задача 3: Как разрезать прямоугольник 4 × 8 на 9 квадратов?

Решение:

Задача 4: По окружности выписаны числа 1, 2, 3. Затем между каждыми двумя соседними числами вставили их сумму (в результате получилось шесть чисел: 1, 3, 2, 5, 3, 4). Потом повторили эту операцию еще 5 раз. Теперь вдоль окружности стоят 192 числа. Найдите их сумму.

Решение: Сумма чисел, вписываемых за один раз, равна удвоенной сумме чисел, имеющихся уже к этому моменту. Значит, после каждой такой операции сумма всех чисел утраивается. После пяти операций сумма всех чисел будет равна 6 • 3⁵.