Задача 1:
Решите уравнение: 5(x² + y² + 1) = 6x + 8y.
Решение:
Перенесем все в левую часть и запишем в виде
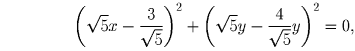
откуда

;
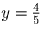
.
Задача 2:
Докажите, что длина медианы, выходящей из тупого угла
треугольника, меньше четверти периметра этого треугольника.
Решение:
Пусть a, b, c – стороны треугольника; γ – тупой угол
(противолежит стороне c); m – медиана. Продолжив медиану на её
длину, получим параллелограмм со сторонами a, b и диагоналями c,
2m. Воспользуемся теоремой косинусов и тем, что угол γ тупой.

Значит, 2m < c. По неравенству
треугольника c < a + b, 2c < a + b + c = P, откуда заключаем, что

.
Задача 3:
Могут ли при некотором вещественном a одновременно быть целыми
числа
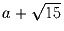
и
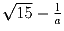
?
Решение:
Да, например, при
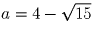
.
Задача 4:


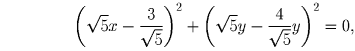
 ;
; 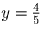 .
.
 .
Задача 3:
Могут ли при некотором вещественном a одновременно быть целыми
числа
.
Задача 3:
Могут ли при некотором вещественном a одновременно быть целыми
числа 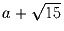 и
и 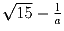 ?
?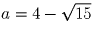 .
Задача 4:
.
Задача 4: