Задача 1:
Задача 2:
M и N – середины сторон BC и CD
параллелограмма ABCD. Доказать, что если DM и AC
перпендикулярны, то BN:CD = 3:2.
Решение:
O – точка пересечения диагоналей ABCD.
CO, DM, BN
пересекаются в одной точке (обозначим её K), как медианы
треугольника BDC. Значит, KN = ⅓BN.
Поскольку гипотенуза прямоугольного
треугольника равна удвоенной медиане, исходящей из прямого угла,
то CD = 2KN. Тогда BN:CD = 3:2.
Задача 3:
Набор из 100 натуральных чисел обладает тем свойством, что
каждое из этих чисел является делителем суммы остальных 99 чисел
этого набора. Могут ли все эти числа быть попарно различными?
Решение:
Рассмотрим числа:
1, 2, …, 2
49; 2
50 – 1, 2 • (2
50 – 1), …,
2
49 • (2
50 – 1), их ровно сто. Сумма этих чисел
S = 2
50 – 1 + (2
50 – 1)(2
50 – 1) = 2
50(2
50 – 1).
S делится
на каждое из наших чисел, значит, сумма любых 99-ти чисел набора
делится на оставшееся, то есть предъявленный набор удовлетворяет
условию задачи.
Задача 4:
Точки O и Q лежат на сторонах MN и MR треугольника
MNR. Отрезки NQ и OR пересекаются в точке P. Докажите,
что площадь треугольника OPQ меньше среднего геометрического
площадей треугольников NOP и PQR.
Решение:
Условие

равносильно неравенству

, которое можно переписать в виде

. А последнее неравенство равносильно
очевидному неравенству
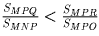
.
Задача 5:
Про вещественные числа x и y известно, что x² – 4xy + 3y² = 7.
Какое
наименьшее значение может принимать выражение
3x² + 2y² – 12(x + y)?
Решение:
3x² + 2y² – 12(x + y) = 3(x – 2)² + 2(y – 3)² – 30 ≥ – 30.
Равенство достигается при x = 2, y = 3 (проверим, что для них
выполнено условие: 2² – 4 • 2 • 3 + 3 • 3² = 7 – верно).


 равносильно неравенству
равносильно неравенству  , которое можно переписать в виде
, которое можно переписать в виде
 . А последнее неравенство равносильно
очевидному неравенству
. А последнее неравенство равносильно
очевидному неравенству 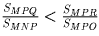 .
Задача 5:
Про вещественные числа x и y известно, что x² – 4xy + 3y² = 7.
Какое
наименьшее значение может принимать выражение
3x² + 2y² – 12(x + y)?
.
Задача 5:
Про вещественные числа x и y известно, что x² – 4xy + 3y² = 7.
Какое
наименьшее значение может принимать выражение
3x² + 2y² – 12(x + y)?