Задача 1:
Задача 2:
Задача 3:
В квадрате ABCD точки K, L, M, N лежат на его сторонах
AB, BC,
CD, DA соответственно. При этом KM || AD, а углы NKL
и LMN прямые. Докажите, что середина отрезка LN совпадает с
центром квадрата ABCD.
Решение:
KLMN – вписанный четырёхугольник с диаметром LN,
значит, середина LN лежит на серединном перпендикуляре к KM и,
следовательно, на серединном перпендикуляре к AD. С другой
стороны, середина LN является серединой боковой стороны трапеции
ABLN и, значит, лежит на средней линии ABLN и, следовательно, на
серединном перпендикуляре к AB. То есть мы получим, что
середина LN является точкой пересечения серединных перпендикуляров
к AB и AD и, следовательно, центром квадрата.
Задача 4:
Сосчитайте значение интеграла:
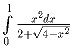
.
Решение:
Заметим, что

, и
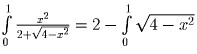
.
Последний интеграл равен площади заштрихованной фигуры, то есть
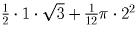
. Таким образом
искомый интеграл равен

.
Задача 5:
Правильная четырехугольная пирамида с двугранным углом при
основании пирамиды, равным 30 вписана в сферу радиуса 1.
Найдите площадь основания пирамиды.
Решение:
Пусть O – центр сферы, O′ – его проекция на
основание пирамиды, a – сторона
основания. Тогда из ∆ O′BM находим, что высота пирамиды
равна
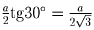
;

. Подставив R = 1,
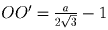
,
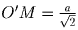
, получим
уравнение относительно a, из которого находим
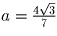
и, следовательно, площадь основания
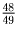
.
ПЕРЕСЧИТАТЬ!!!


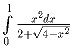 .
. , и
, и 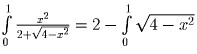 .
Последний интеграл равен площади заштрихованной фигуры, то есть
.
Последний интеграл равен площади заштрихованной фигуры, то есть
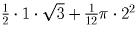 . Таким образом
искомый интеграл равен
. Таким образом
искомый интеграл равен
 .
Задача 5:
Правильная четырехугольная пирамида с двугранным углом при
основании пирамиды, равным 30 вписана в сферу радиуса 1.
Найдите площадь основания пирамиды.
.
Задача 5:
Правильная четырехугольная пирамида с двугранным углом при
основании пирамиды, равным 30 вписана в сферу радиуса 1.
Найдите площадь основания пирамиды.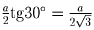 ;
;
 . Подставив R = 1,
. Подставив R = 1,
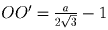 ,
, 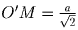 , получим
уравнение относительно a, из которого находим
, получим
уравнение относительно a, из которого находим
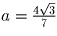 и, следовательно, площадь основания
и, следовательно, площадь основания
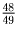 .
.