Задача 1:
На доске написаны числа 9, 11, 13, 15, 17, 19. За ход
разрешается стереть любые два числа, написав вместо них их
сумму, уменьшенную на единицу. Через несколько таких ходов на
доске окажется одно число. Каким оно может быть?
Решение:
С каждым ходом сумма всех написанных на доске чисел уменьшается
на 1. Значит после пяти ходов, когда останется одно число, оно
будет равно 9 + 11 + 13 + 15 + 17 + 19 – 5 = 79.
Задача 2:
Точка M находится на стороне AB, а точка K – на стороне BC
треугольника ABC. Отрезки AK и CM пересекаются в точке O.
Докажите, что если OM = OK и равны углы KAC и MCA, то треугольник
ABC равнобедренный.
Решение:
Так как треугольник AOC равнобедренный,
то AK = MC, а тогда ∆ MCA = ∆ KAC. Значит,
∠ A = ∠ C, откуда BA = BC.
Задача 3:
Маша, Таня и Галя зашли в канцелярский магазин, чтобы купить
карандаши и ручки. Они купили по 10 предметов каждая. Галя купила
в два раза больше ручек, чем Таня карандашей, а Таня в два раза
больше ручек, чем Маша карандашей. Все вместе девочки купили
четное число карандашей. Сколько ручек и сколько карандашей
купила каждая из них?
Решение:
Обозначим через x число купленных Машей карандашей и выразим
через него количества ручек и карандашей, купленных остальными
девочками:

Общее число карандашей
делится на 2, значит, 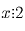 . Так как все
стоящие в таблице числа
положительны, то 2x ≤ 10 и 4x ≥ 10. Всем условиям
удовлетворяет только x = 4. Итак, Таня купила 8 ручек и 2
карандаша, Галя 4 ручки и 6 карандашей, Маша – 6 ручек и 4
карандаша.
. Так как все
стоящие в таблице числа
положительны, то 2x ≤ 10 и 4x ≥ 10. Всем условиям
удовлетворяет только x = 4. Итак, Таня купила 8 ручек и 2
карандаша, Галя 4 ручки и 6 карандашей, Маша – 6 ручек и 4
карандаша.
Задача 4:



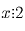 . Так как все
стоящие в таблице числа
положительны, то 2x ≤ 10 и 4x ≥ 10. Всем условиям
удовлетворяет только x = 4. Итак, Таня купила 8 ручек и 2
карандаша, Галя 4 ручки и 6 карандашей, Маша – 6 ручек и 4
карандаша.
. Так как все
стоящие в таблице числа
положительны, то 2x ≤ 10 и 4x ≥ 10. Всем условиям
удовлетворяет только x = 4. Итак, Таня купила 8 ручек и 2
карандаша, Галя 4 ручки и 6 карандашей, Маша – 6 ручек и 4
карандаша.