Задача 1:
Задача 2:
Задача 3:
Существуют ли 19 последовательных чисел, сумма которых делится
на 87?
Решение:
Сумма чисел
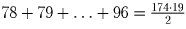
делится на 87.
Задача 4:
На сторонах AB и BC треугольника ABC взяли точки D и E
соответственно, причем BD:DA = BE:EC = 1:2. Отрезки AE и CD
пересекаются в точке O. Докажите, что если OD = OE, то треугольник
ABC – равнобедренный.
Решение:
BD:BA = BE:BC = 1:3, следовательно, DE || AC. Отсюда
заключаем, что ∠ DEO = ∠ EAC и, значит, подобны
треугольники DOE и COA и, так как DO = OE, то AO = OC. Отсюда
получаем равенство треугольников DAC и ECA и, следовательно,
углов A и C треугольника ABC. Значит, AB = BC.
Задача 5:
Найдите все натуральные N такие, что N³ – 7 делится
на N – 2.
Решение:
Заметим, что (n³ – 8) делится на (n – 2). Тогда из того, что
(n³ – 7) делится на (n – 2), следует, что 1 делится на (n – 2).
Значит, n = 3 или n = 1.


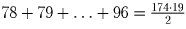 делится на 87.
Задача 4:
На сторонах AB и BC треугольника ABC взяли точки D и E
соответственно, причем BD:DA = BE:EC = 1:2. Отрезки AE и CD
пересекаются в точке O. Докажите, что если OD = OE, то треугольник
ABC – равнобедренный.
делится на 87.
Задача 4:
На сторонах AB и BC треугольника ABC взяли точки D и E
соответственно, причем BD:DA = BE:EC = 1:2. Отрезки AE и CD
пересекаются в точке O. Докажите, что если OD = OE, то треугольник
ABC – равнобедренный.