 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1988 >> Районный тур >> 9 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1988. Районный тур. 9 класс |
|
|
Решение: Если среди чисел sin a2, … , sin an – 1 есть хотя бы одно, не равное 0 (пусть это sin ak), то sin ak – 1 + sin ak + 1 = 2 sin ak. Воспользуемся формулой для суммы синусов:
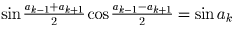 . Отсюда
. Отсюда 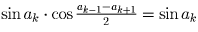 , и тогда
, и тогда
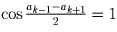 .
Значит ak – 1 – ak + 1 = 4 π m, то есть
разность прогрессии a1,a2, … равна 2 π m. Но это означает, что
sin a1 = sin an – противоречит условию. Таким образом, все члены прогрессии
между sin a1 и sin an равны нулю, в частности,
sin a2 = 0.
Задача 2:
На необитаемом острове пираты закопали клад, причем они
запомнили, что если от Южного Мыса пройти 70 метров налево по
прямой вдоль берега, а затем пройти 110 метров по направлению ко
вкопанному столбу, то окажешься на месте, где зарыт клад. Точно
так же можно попасть на это место, если от Южного Мыса пройти
130 метров к столбу, а затем повернуть направо и пройти 10
метров. Когда пираты вновь приехали на остров, то обнаружили,
что столб вырвало бурей. Как им теперь найти клад?
.
Значит ak – 1 – ak + 1 = 4 π m, то есть
разность прогрессии a1,a2, … равна 2 π m. Но это означает, что
sin a1 = sin an – противоречит условию. Таким образом, все члены прогрессии
между sin a1 и sin an равны нулю, в частности,
sin a2 = 0.
Задача 2:
На необитаемом острове пираты закопали клад, причем они
запомнили, что если от Южного Мыса пройти 70 метров налево по
прямой вдоль берега, а затем пройти 110 метров по направлению ко
вкопанному столбу, то окажешься на месте, где зарыт клад. Точно
так же можно попасть на это место, если от Южного Мыса пройти
130 метров к столбу, а затем повернуть направо и пройти 10
метров. Когда пираты вновь приехали на остров, то обнаружили,
что столб вырвало бурей. Как им теперь найти клад?Решение: Расстояние от Южного мыса до клада по прямой равно
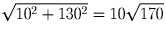 .
Заметим, что сумма квадратов 110² + 70² также
равна
.
Заметим, что сумма квадратов 110² + 70² также
равна 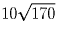 . Значит, если пройти от Южного мыса 70 метров
налево, а потом повернуть под прямым углом направо и пройти 110
метров, то попадешь туда, куда нужно.
Задача 3:
Решить в вещественных числах систему уравнений:
. Значит, если пройти от Южного мыса 70 метров
налево, а потом повернуть под прямым углом направо и пройти 110
метров, то попадешь туда, куда нужно.
Задача 3:
Решить в вещественных числах систему уравнений:
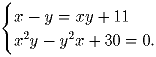
Решение: Обозначив разность и произведение чисел x и y через r и p соответственно, получим
 . Подставив r во второе уравнение, находим,
что r равно 6 или 5, откуда p равно – 5 или – 6 соответственно.
Возвращаясь к старым переменным, получаем решения
системы: (1; – 5), (5; – 1), (2; – 3), (3; – 2).
Задача 4:
Найдите все такие натуральные x, что x³ + 7 делится на x – 2.
. Подставив r во второе уравнение, находим,
что r равно 6 или 5, откуда p равно – 5 или – 6 соответственно.
Возвращаясь к старым переменным, получаем решения
системы: (1; – 5), (5; – 1), (2; – 3), (3; – 2).
Задача 4:
Найдите все такие натуральные x, что x³ + 7 делится на x – 2.Решение: Аналогично задаче 17, заметим что n – 2 является делителем 15. Ответ: x ∈ 1,3,5,7,15.
Задача 5: Микрокалькулятор «Чебурашка» умеет складывать, вычитать и находить по данному числу x обратное к нему число 1/x. Можно ли с помощью этого микрокалькулятора получить число 1, имея число
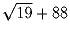 (имеется в виду, что вводить в микрокалькулятор числа,
отличные от данных или полученных в результате вычислений,
запрещается).
(имеется в виду, что вводить в микрокалькулятор числа,
отличные от данных или полученных в результате вычислений,
запрещается).Решение: Получим из числа
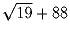 число
число 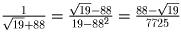 .
Прибавив это число к исходному 7725 раз, получим 176. Затем
получаем
.
Прибавив это число к исходному 7725 раз, получим 176. Затем
получаем 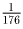 и, сложив его с собой 176 раз, получим
единицу.
и, сложив его с собой 176 раз, получим
единицу.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1988 >> Районный тур >> 9 класс | Убрать решения |