 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Городской тур >> 9 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Городской тур. 9 класс |
|
|
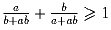 .
.
(Д.~Карпов)
Решение: Домножив на знаменатели, перенеся все в левую часть и приведя подобные члены, перепишем неравенство в виде a² + b² – ab – a²b² ≥ 0. Заметим, что ,
поэтому a²b² ≤ ab ≤ 1. Тогда a² + b² – ab – a²b² ≥ (a – b)² ≥ 0.
,
поэтому a²b² ≤ ab ≤ 1. Тогда a² + b² – ab – a²b² ≥ (a – b)² ≥ 0. Докажите, что
Докажите, что
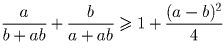 .
.
(С.~Берлов)
Решение: Пусть точка F – середина AB, а точка G – середина BC. Тогда FG = AC/2, как средняя линия. DF = AB/2 и GE = BC/2, поскольку в прямоугольном треугольнике медиана равна половине гипотенузы.Значит, DF + FG + GE равно полупериметру ∆ ABC. Но DE ≤ DF + FG + GE, так как длина ломаной заведомо меньше длины отрезка, соединяющей ее концы.
Задача 3: Решите в натуральных числах уравнение: .
.
(Д.~Карпов)
Решение: Перепишем равенство в виде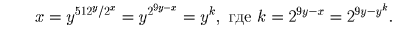
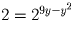 , то есть, 9y – y² = 1, чего не бывает;
k = 3 – не степень двойки;
наконец, при k = 4 из неравенства yk – 1 ≤ 9 находим, что
y = 2, а тогда x = 16. Ответ: x = y = 1 и x = 16, y = 2.
, то есть, 9y – y² = 1, чего не бывает;
k = 3 – не степень двойки;
наконец, при k = 4 из неравенства yk – 1 ≤ 9 находим, что
y = 2, а тогда x = 16. Ответ: x = y = 1 и x = 16, y = 2.Задача 4: Докажите, что количество способов разрезать прямоугольник на уголки из трех клеток вида
 всегда четно.
всегда четно.
(Д.~Карпов)
Решение: Индукция по площади прямоугольника. Пусть для всех прямоугольников меньшей площади утверждение верно. Проведем вертикальную прямую, делящую наш прямоугольник пополам. Все несимметричные относительно нее разбиения очевидным образом разбиваются на пары. При симметричном же разбиении каждая половинка оказывается разбитой на уголки. Значит, число симметричных разбиений исходного прямоугольника равно числу разбиений его «половинки», а оно, по индукционному предположению, четно. Задача 5: В четырехугольнике ABCD на сторонах BC и AD взяты, соответственно, точки R и T. P – точка пересечения отрезков BT и AR; S – точка пересечения отрезков CT и DR. Оказалось, что PRST – параллелограмм. Докажите, что AB || CD.
(Д.~Карпов, А.~Храбров)
Решение: Пусть M – точка пересечения прямых AB и CT. Из параллельности прямых AR и CT следует, что MT:TC = AP:PR. Из параллельности прямых BT и RD следует, что AP:PR = AT:TD. Таким образом, MT:TC = AT:TD, и треугольники ATM и CTD, имеющие равные углы T, подобны. Значит, ∠ AMT = ∠ TCD, поэтому прямые AB и CD параллельны.Задача 6: a, b, c – натуральные числа, причем (a – b) – простое число и 3c² = c(a + b) + ab. Докажите, что 8c + 1 – точный квадрат.
(С.~Берлов)
Решение: Обозначим p = a – b, q = a + b. Тогда имеем 12c² = 4cq + q² – p². Откуда p² = q² + 4cq – 12c² = (q – 2c)(q + 6c). Поскольку p – простое, то q + 6c = p², q – 2c = 1, откуда получаем, что 8c + 1 = p². Задача 7: В государстве 2000 городов. Некоторые пары городов соединены дорогами так, что из любого города можно проехать в любой другой. Докажите, что это государство можно разбить на несколько республик (возможно, всего на одну) так, чтобы в каждой республике из любого города можно было единственным образом проехать в любой другой город этой республики, не выезжая за ее пределы. (В каждой республике должно быть не менее двух городов.)
(Д.~Карпов, А.~Пастор)
Решение: Индукцией по n докажем, что утверждение задачи верно для государств, в которых 2n городов. База очевидна. Переход: пусть это верно для всех государств, состоящих из меньшего числа городов. Если в государстве нет циклов, то все государство можно объявить республикой. Если же циклы есть, то закроем на время несколько дорог так, чтобы цикл остался ровно один. Назовем дороги, из которых состоит цикл, важными, а множество городов в которые можно добраться из города, не проезжая по важной дороге, – окрестностью этого города. Возьмем теперь два города, соединенные важной дорогой (очевидно, их окрестности не пересекаются). Или в окрестности одного из них, или в двух окрестностях вместе будет четное число городов (причем меньшее 2n). Будем считать эти города одной страной, а все остальные – другой, и в каждой стране восстановим закрытые дороги. По построению, обе страны состоят из четного числа городов, и из любого города можно проехать в любой другой в этой стране. По предположению индукции, эти страны можно разбить на республики.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Городской тур >> 9 класс | Убрать решения |