 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Отборочный тур >> 10 КЛАСС. | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Отборочный тур. 10 класс |
|
|
(А.~Голованов)
Решение: Так как (q + 1)(q – 1) делится на p, то одно из чисел q + 1 или q – 1 делится на p. Если q + 1 делится на p, то и p + q + 1 делится на p. Если же q – 1 делится на p, то q = kp + 1 для некоторого натурального k ≤ p. По условию, p² + 1 делится на q, значит, p² + 1 – q = p² – kp = p(p – k) делится на q, значит, p – k делится на q. Следовательно, k = p (иначе 0 < p – k < q), то есть q = p² + 1. Но тогда p + q + 1 = p² + p + 2 – четное число, большее двух. Задача 2: На плоскости даны две пересекающиеся окружности. Точка A – одна из двух точек пересечения этих окружностей. В каждой окружности проведен диаметр, параллельный касательной в точке A к другой окружности, причем эти диаметры не пересекаются. Докажите, что концы этих диаметров лежат на одной окружности.(С.~Берлов )
Решение: Обозначим диаметры BC и DE, а центры соответствующих окружностей – O1 и O2, и проведем из центров окружностей перпендикуляры к соответствующим диаметрам. Пусть эти перпендикуляры пересеклись в точке F (см. рисунок). Докажем, что F – центр искомой окружности.
Заметим, что O1F\|AO2, т. к. O1F и AO2 перпендикулярны BC. Аналогично O2F\|AO1. Значит, AO1FO2 – параллелограмм. Отсюда FO2 = AO1 = BO1, а FO1 = AO2 = DO2. Теперь из равенства треугольников BO1F и FO2D получаем, что FB = FD. Кроме того, точка F, по построению, лежит на серединных перпендикулярах к BC и DE, а значит, FC = FD = FB = FE, что и требовалось.
 Чтобы упростить возможные счетные решения, участникам отбора было
предложено считать, что окружности не содержат внутри себя центров друг
друга. (Приведенное решение не зависит от таких тонкостей.)
Чтобы упростить возможные счетные решения, участникам отбора было
предложено считать, что окружности не содержат внутри себя центров друг
друга. (Приведенное решение не зависит от таких тонкостей.)
(С.~Берлов)
Решение: Рассмотрим в какой-нибудь момент времени систему всех отрезков, соединяющих между собой точки одного цвета. Количество точек, из которых выходит нечетное число этих отрезков, всегда четно, а ведь именно такие точки не меняют цвета при описанной процедуре. Значит, каждую минуту не меняют цвета четное число точек, а меняют цвет – нечетное число. Таким образом, за нечетное число минут происходит нечетное число перекрашиваний отдельных точек, после чего раскраска не может остаться прежней.Задача 4: d1, d2,…,dk – все возможные натуральные делители некоторого натурального числа N, выписанные в порядке возрастания. Оказалось, что d2 – d1, d3 – d2, d4 – d3, …, dk – dk – 1 – также все возможные делители какого-то натурального числа (не обязательно в порядке возрастания). Найдите все N, для которых такое может быть.
(А.~Голованов)
Решение: Число, набор делителей которого образуют разности di + 1 – di, – это наибольшая из разностей, то есть dn – dn – 1. Среди разностей di + 1 – di должна быть единица, поэтому по крайней мере один делитель N четен, так что N четно. Значит, dn – 1 = N/2, dn – dn – 1 = N – N/2 = N/2. Итак, число делителей N/2 ровно на 1 меньше числа делителей N, т. е. все делители N, кроме самого N, являются делителями N/2. Отсюда N – степень двойки, так как если N делится на нечетное число k > 1, то N/2 не может делиться на N/k. Легко проверить, что все степени двойки действительно удовлетворяют условию.Задача 5: В Цветочном городе живут 1995 коротышек. У них имеется 995 10-копеечных монет и неограниченный запас пятаков (монет по 5 коп.). Иногда коротышки меняются монетами: один дает другому монету в 10 копеек, а тот ему – два пятака. Как-то вечером каждый из коротышек заявил: «Сегодня я отдал ровно 10 монет». Докажите, что кто-то из них ошибся.
(К.~Кохась)
Решение: Если кто-то из коротышек обменял два пятака на десятикопеечную монету, а потом разменял эту монету на пятаки, то при совершении этих операций он отдал три монеты (два пятака и эту десятикопеечную). Так как число обменов, совершенных каждым коротышкой за день, на три не делится, то это значит, что каждый из коротышек произвел операцию хотя бы одну операцию обмена, отличную от только что описанной, а именно: либо он выменял себе десятикопеечную монету и никому ее потом не отдал, либо он с самого начала владел десятикопеечной монетой (за которую сегодня он не отдавал пятаков) и разменял ее на пятаки. Таким образом, мы получили, что каждый из коротышек или в самом начале, или в самом конце имеет десятикопеечную монету (а может, и в начале, и в конце). Но этого не может быть, т. к. десятикопеечных монет слишком мало. Значит, кто-то из коротышек ошибся. Докажите, что если у коротышек было 1329 десятикопеечных монет,
то все равно, кто-то из них ошибся.
Докажите, что если у коротышек было 1329 десятикопеечных монет,
то все равно, кто-то из них ошибся.
(С.~Берлов)
Решение: Пусть AL и CK – высоты ∆ ABC. Продолжим отрезок HD за точку D и отложим отрезок DH′ = HD. Тогда четырехугольник AHCH′ – параллелограмм, так как его диагонали делятся точкой пересечения пополам. Отсюда следует, что H′A\|CK, а значит, ∠ H′AB = 90. Четырехугольник AEHH′ – вписанный, так как ∠ H′AE = ∠ EHH′ = 90, поэтому углы H′EH и H′AH равны. Аналогично ∠ H′CH = ∠ H′FH. Но ∠ H′AH и ∠ H′CH равны как противоположные углы параллелограмма, значит, ∠ H′EH = ∠ H′FH. Таким образом ∆ EH′F равнобедренный, и его высота H′H является медианой, то есть, EH = HF.Решение 2. Пусть L – основание высоты, опущенной из вершины A. Тогда ∠ AHD = 90 – ∠ AHE = 90 – ∠ LHF = ∠ LFH = ∠ BFH. Кроме того, ∠ HAD = ∠ FBH = 90 – ∠ C. Следовательно, ∆ AHD ∽ ∆ BFH. Аналогично доказывается, что ∆ CHD ∽ ∆ BEH. Значит,
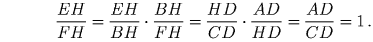
Решение 3 (найдено одним из участников олимпиады). Через точку A проведем прямую, параллельную EF, пусть она пересекает сторону BC в точке M (Если она пересекает продолжение стороны BC, то сделаем аналогичное построение для вершины C). Тогда AM ⊥ HD. Пусть высота BG (проходящая через точку H) пересекает отрезок AM в точке N. Достаточно доказать, что AN = NM, тогда результат задачи будет следовать из теоремы Фалеса. Для этого, в свою очередь, достаточно проверить, что прямая DN совпадает со средней линией ∆ ABC, или просто что DN || BC. Но прямая DN проходит через точку пересечения высот ∆ AHD. Поэтому DN ⊥ AH, а прямая AH – это высота ∆ ABC, так что DN || BC.
 Утверждение задачи является также простым следствием теоремы о
бабочке (См. Г. Коксетер, С. Грейтцер «Новые встречи с геометрией»;
Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом «Избранные задачи и теоремы
планиметрии», задача 122.).
Утверждение задачи является также простым следствием теоремы о
бабочке (См. Г. Коксетер, С. Грейтцер «Новые встречи с геометрией»;
Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом «Избранные задачи и теоремы
планиметрии», задача 122.).
Задача 7: Найдите все простые p и q, для которых p² – p + 1 = q³.
(А.~Голованов)
Решение: Ответ: p = 19, q = 7. Вычтем из обоих частей уравнения единицу: p(p – 1) = (q – 1)(q² + q + 1). Поскольку p – простое, один из множителей справа делится на p. Но q – 1 не может делиться на p, так как q < p. Значит, q² + q + 1 = kp и p – 1 = k(q – 1) для некоторого натурального k. Выражая p из второго равенства и подставляя в первое, получаем уравнение k²(q – 1) + k = q² + q + 1. Из него следует, что k² > q + 1 (иначе k²(q – 1) + k ≤ q² + k – 1 < q² + q + 1) и k² < q + 3 (иначе k > 2 и k²(q – 1) + k ≥ q² + 2q + k – 3 > q² + q + 1). Следовательно, k² = q + 2, q² + q + 1 = (q + 2)(q – 1) + k = q² + q + k – 2, откуда k = 3. Значит, q = k² – 2 = 7, p = k(q – 1) + 1 = 19. Условие простоты q в приведенном решении не использовалось.
Условие простоты q в приведенном решении не использовалось.
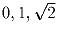 . Разрешается к любому из этих
чисел прибавить разность двух других, умноженную на произвольное рациональное
число. Можно ли такими операциями получить числа
. Разрешается к любому из этих
чисел прибавить разность двух других, умноженную на произвольное рациональное
число. Можно ли такими операциями получить числа 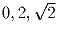 ?
?
(С.~Иванов)
Решение: Все числа, получаемые в процессе выполнения операций, имеют вид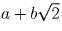 , где a и b – рациональные числа,
причем представление числа в таком виде единственно, поскольку
, где a и b – рациональные числа,
причем представление числа в таком виде единственно, поскольку
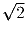 – иррациональное число. Поставим числу
– иррациональное число. Поставим числу 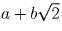 в соответствие точку (a,b) на координатной плоскости и будем
следить за треугольником, полученным таким способом из трех
написанных на доске чисел. Прибавление к одному из чисел разности
двух других, умноженной на рациональное число r, соответствует
переносу одной из вершин треугольника на вектор противолежащей стороны,
умноженный на r. При такой операции площадь треугольника не изменяется.
Числам
в соответствие точку (a,b) на координатной плоскости и будем
следить за треугольником, полученным таким способом из трех
написанных на доске чисел. Прибавление к одному из чисел разности
двух других, умноженной на рациональное число r, соответствует
переносу одной из вершин треугольника на вектор противолежащей стороны,
умноженный на r. При такой операции площадь треугольника не изменяется.
Числам 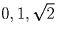 соответствует треугольник площади 1/2, а числам
соответствует треугольник площади 1/2, а числам
 – треугольник площади 1. Значит, получить второй набор
из первого невозможно.
– треугольник площади 1. Значит, получить второй набор
из первого невозможно.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Отборочный тур >> 10 КЛАСС. | Убрать решения |