Задача 1: p и q – простые числа, такие, что p² + 1 делится на q, а q² – 1 делится на p. Докажите, что p + q + 1 – составное число.

(А.~Голованов)

Решение: Так как (q + 1)(q – 1) делится на p, то одно из чисел q + 1 или q – 1 делится на p. Если q + 1 делится на p, то и p + q + 1 делится на p. Если же q – 1 делится на p, то q = kp + 1 для некоторого натурального k ≤ p. По условию, p² + 1 делится на q, значит, p² + 1 – q = p² – kp = p(p – k) делится на q, значит, p – k делится на q. Следовательно, k = p (иначе 0 < p – k < q), то есть q = p² + 1. Но тогда p + q + 1 = p² + p + 2 – четное число, большее двух.

Задача 2: Дан треугольник ABC. На продолжении стороны AB за точку B, на продолжении BC за точку C и на продолжении стороны CA за точку A выбраны точки B₁, C₁, A₁ соответственно, так, что AB = BB₁, BC = CC₁, CA = AA₁. Оказалось, что треугольник A₁B₁C₁ – равносторонний. Докажите, что треугольник ABC – тоже равносторонний.

(Д.~Карпов)

Решение: Решение 1. Проведем отрезки A₁B, B₁C, C₁A. Треугольник A₁B₁C₁ разбит на 7 маленьких треугольничков. Нетрудно заметить, что все они одинаковой площади. Поэтому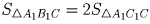 Проведем высоты B₁M и C₁P этих треугольников к их общей стороне A₁C, и пусть N – точка пересечения прямой A₁C с отрезком B₁C₁. Тогда B₁M = 2C₁P и треугольники B₁MN и C₁NP подобны с коэффициентом подобия 2. Значит, прямая A₁C делит отрезок B₁C₁ в отношении 2:1. Аналогично, прямые B₁A и C₁B делят соответственно отрезки C₁A₁ и  A₁B₁ в отношении 2:1. Следовательно, при повороте на 120 вокруг центра треугольника A₁B₁C₁ вся картинка переходит в себя, и значит,  ∆ ABC – правильный.

Решение 2. Обозначим стороны треугольника ABC через a, b, c, а сторону треугольника A₁B₁C₁ – через l. Выразим из теорем косинусов для треугольников ABC и A₁AB косинус угла CAB:

Отсюда 3b² + 6c² – 2a² = l². Поступая аналогично для других углов треугольника ABC, мы придем к линейной относительно a², b², c² системе уравнений:

и, решая ее, найдем, что a² = b² = c² = l²/7.

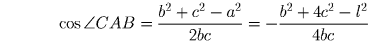
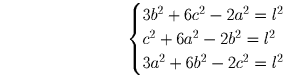
Задача 3: a,b,c,d > 0. Докажите неравенство:

(ac + bd)⁵ + (ad + bc)⁵ ≤ (a + b)⁵(c⁵ + d⁵)

(А.~Храбров)

Решение: Решение 1. Поделим левую и правую части доказываемого неравенства на (a + b)⁵: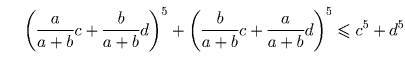

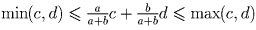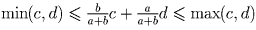Заметим, что суммы выражений, возводимых в пятую степень в левой и правой части получившегося неравенства, равны c + d, и при этом , . Тогда неравенство следует из следующего стандартного утверждения:

Лемма. Пусть x ≥ y ≥ 0, (x – y)/2 ≥ t ≥ 0. Тогда x⁵ + y⁵ ≥ (x – t)⁵ + (y + t)⁵, иными словами, при фиксированной сумме двух неотрицательных чисел, сумма их пятых степеней будет максимальна тогда, когда максимальна разность этих чисел.

Доказательство. Соберем слагаемые, содержащие x, в правой части, а слагаемые, содержащие y, – в левой, и разложим на множители. Получим:

Это неравенство очевидно, поскольку в левой части каждое слагаемое не меньше соответствующего слагаемого в правой.

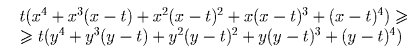
Решение 2. Заметим, что при a = 0 левая часть доказываемого неравенства равна правой. Поэтому достаточно доказать, что при a ≥ 0 производная (по a) левой части не превосходит производную правой, т. е. c(ac + bd)⁴ + d(ad + bc)⁴ ≤ (a + b)⁴(c⁵ + d⁵) При a = 0 имеем верное неравенство cd⁴ + dc⁴ ≤ c⁵ + d⁵, которое мгновенно доказывается разложением на множители (а знатоки или снобы скажут: «неравенство Мюрхеда»). Поэтому достаточно доказать неравенство между производными по a левой и правой части последнего неравенства: c²(ac + bd)³ + d²(ad + bc)³ ≤ (a + b)³(c⁵ + d⁵) Продолжая в том же духе, после пятого дифференцирования мы получим очевидное неравенство c⁵ + d⁵ ≤ c⁵ + d⁵, которое доказывает все предыдущие (и, в том числе, исходное) неравенства.

Задача 4: Можно ли расставить по окружности числа от 1 до 25 так, чтобы сумма любых пяти стоящих подряд чисел давала при делении на 5 остаток 1 или 4?

(Р.~Семизаров)

Решение: Нет, нельзя. Допустим, однако, что это возможно. Разобьем числа на пять групп по пять подряд стоящих чисел. По условию, сумма чисел в каждой группе дает остаток  ± 1 при делении на 5, но при этом сумма всех чисел, очевидно, на 5 делится. Такое может быть лишь в том случае, если суммы чисел во всех пяти группах дают остаток 1 при делении на 5 или все эти суммы дают остаток  – 1.

Теперь рассмотрим «соседнее» разбиение на группы, получающееся из исходного сдвигом по часовой стрелке на одно место. Отметим числа, стоящие в начале каждой группы первого разбиения (см. рис.). Возможны два случая:

1 случай. Суммы чисел одной группы в первом и втором разбиении дают одинаковый остаток при делении на 5 (обе  + 1 или обе  – 1). Тогда, очевидно, отмеченные числа должны давать одинаковый остаток при делении на 5.

2 случай. Суммы чисел одной группы в первом и втором разбиении дают разные остатки при делении на 5, скажем, в первой –  + 1, а во второй –  – 1. Тогда каждое следующее по часовой стрелке отмеченное число дает остаток «на два меньший», чем предыдущее, и все пять отмеченных чисел дают пять различных остатков при делении на 5.

Поскольку среди всех наших двадцати пяти чисел нет шести, дающих одинаковые остатки при делении на 5, то случай 1 и случай 2 взаимно исключают друг друга в том смысле, что если для каких-либо двух соседних разбиений имеет место случай 1, то ни для каких двух других соседних разбиений не может иметь место случай 2 и наоборот. Значит, либо любые два соседних разбиения имеют одинаковые остатки сумм чисел в группах, либо любые два соседних разбиения имеют противоположные остатки сумм чисел в группах. В первом случае числа, расположенные через четыре, всегда дают одинаковый остаток, а значит, в любой пятерке подряд стоящих чисел все числа дают разные остатки, но тогда сумма чисел в любой пятерке делится на 5, что противоречит условию. А во втором случае при сдвиге разбиения на одно место по часовой стрелке остаток суммы чисел в любой группе этого разбиения меняется на противоположный. Выполняя последовательно пять сдвигов, мы придем к исходному разбиению, но обнаружим при этом, что у остатка суммы изменился знак, чего быть на может. Наше предположение оказалось неверным.

Задача 5: В Цветочном городе живут 1995 коротышек. У них имеется 995 10-копеечных монет и неограниченный запас пятаков (монет по 5 коп.). Иногда коротышки меняются монетами: один дает другому монету в 10 копеек, а тот ему – два пятака. Как-то вечером каждый из коротышек заявил: «Сегодня я отдал ровно 10 монет». Докажите, что кто-то из них ошибся.

(К.~Кохась)

Решение: Если кто-то из коротышек обменял два пятака на десятикопеечную монету, а потом разменял эту монету на пятаки, то при совершении этих операций он отдал три монеты (два пятака и эту десятикопеечную). Так как число обменов, совершенных каждым коротышкой за день, на три не делится, то это значит, что каждый из коротышек произвел операцию хотя бы одну операцию обмена, отличную от только что описанной, а именно: либо он выменял себе десятикопеечную монету и никому ее потом не отдал, либо он с самого начала владел десятикопеечной монетой (за которую сегодня он не отдавал пятаков) и разменял ее на пятаки. Таким образом, мы получили, что каждый из коротышек или в самом начале, или в самом конце имеет десятикопеечную монету (а может, и в начале, и в конце). Но этого не может быть, т. к. десятикопеечных монет слишком мало. Значит, кто-то из коротышек ошибся.

Докажите, что если у коротышек было 1329 десятикопеечных монет, то все равно, кто-то из них ошибся.

Задача 6: M – некоторое множество простых чисел, в котором больше одного элемента. Известно, что для всякого (конечного) подмножества N ⊂ M число 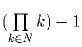имеет простые делители только из M. Докажите, что M совпадает с множеством всех простых чисел.

(А.~Пастор)

Решение: Допустим, что простое число p не принадлежит множеству M. Множество M бесконечно, поскольку в противном случае произведение его элементов, уменьшенное на единицу, будет взаимно просто с каждым из элементов M, что противоречит условию. Выберем в M простые числа q₁,q₂, … ,q_p, дающие одинаковые остатки при делении на p. Рассмотрим p чисел: q₁, q₁q₂, q₁q₂q₃, …, q₁q₂ … q_p. Среди них найдутся два, дающие одинаковый остаток при делении на p. Разность этих двух чисел имеет вид q₁q₂ … q_k(q_k + 1 … q_m – 1) (1 ≤ k < m ≤ p) и делится на p, значит, (q_k + 1 … q_m – 1) делится на p. Но тогда p ∈ M.

Задача 7: В остроугольном треугольнике ABC проведены высоты AA₁ и BB₁. На (меньшей) дуге AB описанной около треугольника окружности выбрана точка L, такая, что LC = CB. При этом оказалось, что  ∠ BLB₁ = 90. Докажите, что высота AA₁ делится высотой BB₁ пополам.

(С.~Берлов)

Решение: Пусть H – точка пересечения высот,  α ,  β ,  γ  — углы  ∆ ABC. Заметим, что  ∠ LBC =  ∠ BAC =  α  как углы опирающиеся на равные хорды. Тогда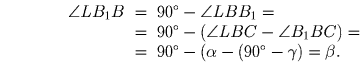

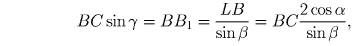
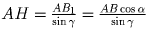Так как  ∆ LCB – равнобедренный с углом  α  при основании, то LB = 2BC cos  α . Тогда

и, значит, углы  ∆ ABC удовлетворяют соотношению  sin  γ  sin  β  = 2 cos  α . Теперь легко получить утверждение задачи:  ∠ AHB₁ =  γ  как угол между высотами, поэтому ; с другой стороны, очевидно, что AA₁ = AB sin  β . Осталось применить выведенное соотношение между углами треугольника.