 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Отборочный тур >> 9 КЛАСС | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Отборочный тур. 9 класс |
|
|
(А.~Голованов)
Решение: Так как (q + 1)(q – 1) делится на p, то одно из чисел q + 1 или q – 1 делится на p. Если q + 1 делится на p, то и p + q + 1 делится на p. Если же q – 1 делится на p, то q = kp + 1 для некоторого натурального k ≤ p. По условию, p² + 1 делится на q, значит, p² + 1 – q = p² – kp = p(p – k) делится на q, значит, p – k делится на q. Следовательно, k = p (иначе 0 < p – k < q), то есть q = p² + 1. Но тогда p + q + 1 = p² + p + 2 – четное число, большее двух.Задача 2: a,b,c > 0. Докажите неравенство:
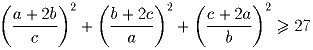
(Д.~Карпов)
Решение: Применим к числителям неравенство о среднем арифметическом и среднем геометрическом для трех чисел, рассматривая, например, 2a как a + a, а затем это же неравенство о средних к сумме полученных дробей. Получаем:
Задача 3: На плоскости даны две пересекающиеся окружности. Точка A – одна из двух точек пересечения этих окружностей. В каждой окружности проведен диаметр, параллельный касательной в точке A к другой окружности, причем эти диаметры не пересекаются. Докажите, что концы этих диаметров лежат на одной окружности.
(С.~Берлов )
Решение: Обозначим диаметры BC и DE, а центры соответствующих окружностей – O1 и O2, и проведем из центров окружностей перпендикуляры к соответствующим диаметрам. Пусть эти перпендикуляры пересеклись в точке F (см. рисунок). Докажем, что F – центр искомой окружности.
Заметим, что O1F\|AO2, т. к. O1F и AO2 перпендикулярны BC. Аналогично O2F\|AO1. Значит, AO1FO2 – параллелограмм. Отсюда FO2 = AO1 = BO1, а FO1 = AO2 = DO2. Теперь из равенства треугольников BO1F и FO2D получаем, что FB = FD. Кроме того, точка F, по построению, лежит на серединных перпендикулярах к BC и DE, а значит, FC = FD = FB = FE, что и требовалось.
 Чтобы упростить возможные счетные решения, участникам отбора было
предложено считать, что окружности не содержат внутри себя центров друг
друга. (Приведенное решение не зависит от таких тонкостей.)
Чтобы упростить возможные счетные решения, участникам отбора было
предложено считать, что окружности не содержат внутри себя центров друг
друга. (Приведенное решение не зависит от таких тонкостей.)
(С.~Берлов)
Решение: Рассмотрим в какой-нибудь момент времени систему всех отрезков, соединяющих между собой точки одного цвета. Количество точек, из которых выходит нечетное число этих отрезков, всегда четно, а ведь именно такие точки не меняют цвета при описанной процедуре. Значит, каждую минуту не меняют цвета четное число точек, а меняют цвет – нечетное число. Таким образом, за нечетное число минут происходит нечетное число перекрашиваний отдельных точек, после чего раскраска не может остаться прежней.Задача 5: Пусть M – множество значений многочлена x² + 1 в целых точках. Докажите, что множество M не содержит ни одной бесконечной (непостоянной) геометрической прогрессии.
(А.~Голованов)
Решение: Пусть (an) – некоторая геометрическая прогрессия, содержащаяся в M. Пусть q – знаменатель этой прогрессии, он, очевидно, натурален. Пусть ai = b² + 1 – член последовательности, такой, что b > q (!). Тогда ai + 2 = q²ai. Если ai + 2 = c² + 1, то получаем: c² + 1 = b²q² + q², откуда q² – 1 = c² – (qb)² = (c + qb)(c – qb) ≥ c + qb ≥ q²\,. Противоречие.Задача 6: Прямоугольник разбит на доминошки (т. е. прямоугольники 1 × 2). Докажите, что его клетки можно раскрасить в два цвета так, чтобы любая доминошка в данном разбиении содержала клетки разных цветов, но в любом другом разбиении этого прямоугольника на доминошки нашлась бы доминошка, содержащая две клетки одного цвета.
(Д.~Карпов)
Решение: Решение 1. Покажем, что утверждение задачи верно не только для прямоугольника, но и для любой клетчатой фигуры, которую можно разбить на доминошки. Индукция по числу доминошек разбиения. Пусть для всех меньших фигур это верно. Рассмотрим «угловую» клетку, у которой нет соседа ни слева, ни сверху (такую клетку можно накрыть доминошкой ровно двумя способами), и раскрасим по индукционному предположению всю фигуру без доминошки разбиения, содержащей эту клетку. Покрасим теперь оставшуюся доминошку в два цвета так, чтобы наша клетка была того же цвета, что и ее сосед, не содержащийся в этой доминошке (если такого соседа нет – то доминошку можно раскрасить как угодно). Получившаяся раскраска удовлетворяет условию. Действительно, если в каком-либо другом разбиении доминошка, накрывающая нашу угловую клетку, расположена так же, как в рассмотренном, то, по индукционному предположению, в оставшейся части фигуры найдется «одноцветная» доминошка, если же угловая клетка накрыта доминошкой вторым способом, то уже в этой доминошке обе клетки одного цвета.Решение 2 (найдено одним из участников олимпиады). Предъявим требуемую раскраску. Для каждой горизонтальной доминошки покрасим в черный цвет левую занимаемую ею клетку, а для каждой вертикальной – нижнюю. Введем систему координат, в которой координаты центров клеток целочисленны, а оси направлены стандартным образом: вверх и вправо. Пусть S – разность суммы координат центров всех белых клеток и суммы координат центров всех черных. В исходной расстановке каждая доминошка вносит в эту сумму вклад, равный + 1, поэтому S равно количеству доминошек. Допустим, что у нас есть какое-то другое разбиение, в котором каждая доминошка содержит по одной черной и одной белой клетке построенной раскраски. Так как величина S зависит только от раскраски, а вклад каждой доминошки нового разбиения не превосходит единицы, мы заключаем, что все вклады равны единице, то есть в каждой доминошке нового разбиения черная клетка тоже находится слева или снизу. Но расположение доминошек с таким свойством однозначно восстанавливается по имеющейся раскраске (рассмотрите, например, снизу вверх самый левый столбец клеток, потом следующий и т. д.) и, следовательно, совпадает с исходным.
Задача 7: H – ортоцентр остроугольного треугольника ABC; D – середина стороны AC. Прямая, проходящая через H перпендикулярно отрезку DH, пересекает стороны AB и BC в точках E и F. Докажите, что HE = HF.(С.~Берлов)
Решение: Пусть AL и CK – высоты ∆ ABC. Продолжим отрезок HD за точку D и отложим отрезок DH′ = HD. Тогда четырехугольник AHCH′ – параллелограмм, так как его диагонали делятся точкой пересечения пополам. Отсюда следует, что H′A\|CK, а значит, ∠ H′AB = 90. Четырехугольник AEHH′ – вписанный, так как ∠ H′AE = ∠ EHH′ = 90, поэтому углы H′EH и H′AH равны. Аналогично ∠ H′CH = ∠ H′FH. Но ∠ H′AH и ∠ H′CH равны как противоположные углы параллелограмма, значит, ∠ H′EH = ∠ H′FH. Таким образом ∆ EH′F равнобедренный, и его высота H′H является медианой, то есть, EH = HF.Решение 2. Пусть L – основание высоты, опущенной из вершины A. Тогда ∠ AHD = 90 – ∠ AHE = 90 – ∠ LHF = ∠ LFH = ∠ BFH. Кроме того, ∠ HAD = ∠ FBH = 90 – ∠ C. Следовательно, ∆ AHD ∽ ∆ BFH. Аналогично доказывается, что ∆ CHD ∽ ∆ BEH. Значит,
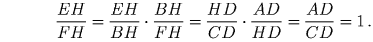
Решение 3 (найдено одним из участников олимпиады). Через точку A проведем прямую, параллельную EF, пусть она пересекает сторону BC в точке M (Если она пересекает продолжение стороны BC, то сделаем аналогичное построение для вершины C). Тогда AM ⊥ HD. Пусть высота BG (проходящая через точку H) пересекает отрезок AM в точке N. Достаточно доказать, что AN = NM, тогда результат задачи будет следовать из теоремы Фалеса. Для этого, в свою очередь, достаточно проверить, что прямая DN совпадает со средней линией ∆ ABC, или просто что DN || BC. Но прямая DN проходит через точку пересечения высот ∆ AHD. Поэтому DN ⊥ AH, а прямая AH – это высота ∆ ABC, так что DN || BC.
 Утверждение задачи является также простым следствием теоремы о
бабочке (См. Г. Коксетер, С. Грейтцер «Новые встречи с геометрией»;
Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом «Избранные задачи и теоремы
планиметрии», задача 122.).
Утверждение задачи является также простым следствием теоремы о
бабочке (См. Г. Коксетер, С. Грейтцер «Новые встречи с геометрией»;
Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом «Избранные задачи и теоремы
планиметрии», задача 122.).
Задача 8: Существует ли возрастающая последовательность натуральных чисел
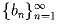 такая, что при всех натуральных n сумма цифр
числа
такая, что при всех натуральных n сумма цифр
числа 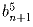 равна числу
равна числу 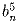 ?
?
(Д.~Давыдок, Д.~Карпов)
Решение: Ответ: да, такая последовательность существует. Ищем элементы последовательности среди чисел вида 10k – 1.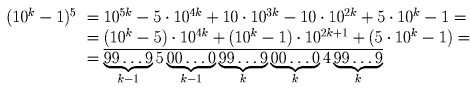
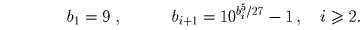
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Отборочный тур >> 9 КЛАСС | Убрать решения |