 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 10 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Районный тур. 10 класс |
|
|
(С.~Берлов)
Решение: Ответ: наибольшая возможная сумма цифр – 51 – у числа 999888, наименьшая возможная сумма цифр – 5 – у числа 100112. Задача 2: На острове Невезения, где живут только рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут, существуют три политических партии, причем каждый житель состоит ровно в одной из них. Каждому жителю задали три вопроса: состоите ли вы в первой, состоите ли во второй, состоите ли в третьей партии. На эти вопросы было получено 60%, 50%, 40% [60%, 40%, 30%] утвердительных ответов соответственно. Кого во второй [третьей] партии больше: рыцарей или лжецов?
(Ф.~Назаров)
Решение: Каждый рыцарь ответил утвердительно ровно на один вопрос, а каждый лжец – ровно на два. Общее количество утвердительных ответов равно 150% (от всего населения острова). Значит, 50% населения острова составляют лжецы. Утвердительно на вопрос о принадлежности ко второй партии ответили рыцари из второй партии и лжецы, не состоящие во второй партии. Если рыцари из второй партии составляют n% населения острова, то лжецы не из второй партии составляют (50 – n)% населения, а лжецы, состоящие во второй партии, составляют (50 – (50 – n)) = n% населения. Т. е. во второй партии лжецов и рыцарей поровну.Второй вариант решается аналогично. Ответ: поровну.
Задача 3: В ромбе ABCD на отрезке BC нашлась точка E, такая, что AE = CD. Отрезок ED пересекается с описанной окружностью треугольника AEB в точке F. Докажите, что точки A, F и C лежат на одной прямой.[В ромбе ABCD описанная окружность треугольника BCD пересекает сторону AB в точке E, описанная окружность треугольника AED пересекает отрезок BD в точке F. Докажите, что точки E, F и C лежат на одной прямой.]
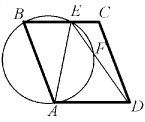
(С.~Берлов)
Решение: Так как четырехугольник ABEF вписанный, то сумма углов BEF и BAF равна 180. Заметим, что сумма углов BEF и FEC также равна 180. Поэтому ∠ BAF = ∠ FEC. Далее, так как трапеция AECD – равнобочная, то ∠ FEC = ∠ ACE, а поскольку треугольник ABC – равнобедренный, то ∠ ACE = ∠ BAC. Мы получили, что ∠ BAF = ∠ BAC, откуда и следует требуемое.Второй вариант: Так как четырехугольник AEFD вписанный, то сумма углов AEF и ADF равна 180. Заметим, что сумма углов AEF и FEB также равна 180. Поэтому ∠ ADF = ∠ FEB. Диагональ ромба является биссектрисой его угла, поэтому ∠ ADF = ∠ BDC. Далее, так как трапеция DEBC – вписанная, то ∠ BDC = ∠ BEC, как опирающиеся на одну дугу. Мы получили, что ∠ BEF = ∠ BEC, откуда и следует требуемое.
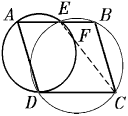
Задача 4: Рассмотрим точки трехмерного пространства, координаты которых целочисленны и удовлетворяют неравенствам: 0 < x < 100, 0 < y < 100, 0 < z < 100. Для каждой такой точки напишем сумму ее наибольшей и наименьшей координаты. Чему равна сумма всех написанных чисел?
[ …0 < x,y,z < 200. Для каждой точки напишем её среднюю по величине координату. Чему равна сумма всех написанных чисел?]
(Р.~Исмаилов)
Решение: Разобьем все точки, кроме точки (50,50,50), на пары, симметричные относительно нее: пару с точкой (x,y,z) образует точка (100 – x,100 – y,100 – z). Сумма чисел, выписанных для каждой пары, равна двумстам, количество пар равно (99³ – 1)/2. Значит, искомая сумма равна (99³ – 1) • 100 + 100 (последнее слагаемое соответствует центральной точке). Задача 5: x и y – вещественные числа из отрезка [0,1]. Докажите неравенство: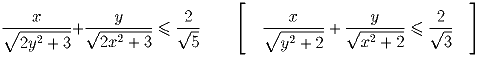
(А.~Голованов)
Решение: Решение 1. Воспользуемся неравенством о среднем арифметическом и среднем квадратичном двух чисел: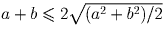 (которое легко
доказывается возведением в квадрат), применив его
к левой части данного неравенства. Получим:
(которое легко
доказывается возведением в квадрат), применив его
к левой части данного неравенства. Получим:
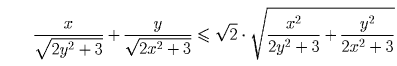
Решение 2. Не умаляя общности, можно считать, что x ≤ y. Тогда
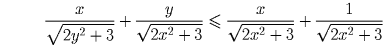
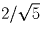 . Возведем в квадрат и выполним
преобразования, получим: 3x² – 10x + 7 ≥ 0, что верно при x ∈ [0,1].
. Возведем в квадрат и выполним
преобразования, получим: 3x² – 10x + 7 ≥ 0, что верно при x ∈ [0,1].
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 10 класс | Убрать решения |