 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 11 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада 1995 года. Районный тур. 11 класс |
|
|
(Ф.~Назаров)
Решение: Каждый рыцарь ответил утвердительно ровно на один вопрос, а каждый лжец – ровно на два. Общее количество утвердительных ответов равно 150% (от всего населения острова). Значит, 50% населения острова составляют лжецы. Утвердительно на вопрос о принадлежности ко второй партии ответили рыцари из второй партии и лжецы, не состоящие во второй партии. Если рыцари из второй партии составляют n% населения острова, то лжецы не из второй партии составляют (50 – n)% населения, а лжецы, состоящие во второй партии, составляют (50 – (50 – n)) = n% населения. Т. е. во второй партии лжецов и рыцарей поровну.Второй вариант решается аналогично. Ответ: поровну.
Задача 2: Можно ли в таблице 3 × 3 расставить числа
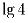 ,
,
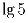 , …,
, …, 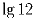 [
[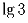 ,
, 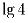 , …,
, …, 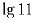 ] так,
чтобы множество сумм чисел этой таблицы по строкам совпадало со
множеством сумм чисел по столбцам?
] так,
чтобы множество сумм чисел этой таблицы по строкам совпадало со
множеством сумм чисел по столбцам?
(А.~Храбров)
Решение: Да, можно.1 вариант:

2 вариант:

Задача 3: В ромбе ABCD на отрезке BC нашлась точка E, такая, что AE = CD. Отрезок ED пересекается с описанной окружностью треугольника AEB в точке F. Докажите, что точки A, F и C лежат на одной прямой.
[В ромбе ABCD описанная окружность треугольника BCD пересекает сторону AB в точке E, описанная окружность треугольника AED пересекает отрезок BD в точке F. Докажите, что точки E, F и C лежат на одной прямой.]
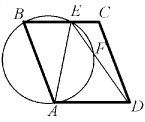
(С.~Берлов)
Решение: Так как четырехугольник ABEF вписанный, то сумма углов BEF и BAF равна 180. Заметим, что сумма углов BEF и FEC также равна 180. Поэтому ∠ BAF = ∠ FEC. Далее, так как трапеция AECD – равнобочная, то ∠ FEC = ∠ ACE, а поскольку треугольник ABC – равнобедренный, то ∠ ACE = ∠ BAC. Мы получили, что ∠ BAF = ∠ BAC, откуда и следует требуемое.Второй вариант: Так как четырехугольник AEFD вписанный, то сумма углов AEF и ADF равна 180. Заметим, что сумма углов AEF и FEB также равна 180. Поэтому ∠ ADF = ∠ FEB. Диагональ ромба является биссектрисой его угла, поэтому ∠ ADF = ∠ BDC. Далее, так как трапеция DEBC – вписанная, то ∠ BDC = ∠ BEC, как опирающиеся на одну дугу. Мы получили, что ∠ BEF = ∠ BEC, откуда и следует требуемое.
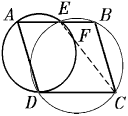
Задача 4: x и y – вещественные числа из отрезка [0,1/2]. Докажите неравенство:
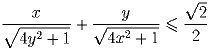
[ x и y – вещественные числа из отрезка [0,2]. Докажите неравенство:
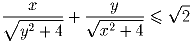
(А.~Голованов)
Решение: Решение 1. По неравенству о среднем арифметическом и среднем квадратичном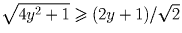 . Поэтому
. Поэтому
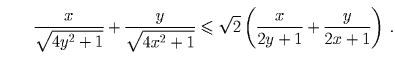
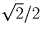 .
.Решение 2. Положим x = ½ tg α , y = ½ tg β , α , β ∈ [0, π /4]. Тогда исходное неравенство примет вид:
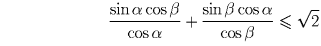
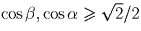 , то достаточно доказать неравенство
, то достаточно доказать неравенство
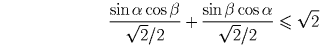
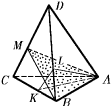
Задача 5: Дан тетраэдр ABCD. Плоскость γ делит пополам двугранный угол при ребре AB и пересекает ребро CD в точке M. При этом оказалось, что отрезок BM – биссектриса угла B треугольника BCD. На ребрах BC и BD выбраны точки K и L, такие, что отрезки AK и AL – высоты треугольников ABC и ABD соответственно. Докажите, что прямая KL перпендикулярна плоскости γ .
(М.~Пратусевич, К.~Кохась)
Решение: Рассмотрим отношение объемов тетраэдров ABDM и ABCM. С одной стороны, так как точка M принадлежит биссекторной плоскости, то длины перпендикуляров, опущенных из нее на плоскости ABD и ABC, равны, и поэтому V(ABDM):V(ABCM) = S(ABD):S(ABC). С другой стороны, эти тетраэдры имеют общую высоту из вершины B к плоскости ADC, и поэтому V(ABDM):V(ABCM) = S(ADM):S(AMC) = DM:MC = BD:BC, где в последнем равенстве мы воспользовались свойством биссектрисы BM.Сопоставляя эти два наблюдения, заключаем, что S(ABD):S(ABC) = BD:BC, откуда следует, что AL = AK. Таким образом, прямоугольные треугольники ABL и AKB равны по катету и гипотенузе. Значит, ∠ ABK = ∠ ABL и BK = BL. При симметрии относительно плоскости γ плоскость ABC переходит в плоскость ABD, а так как ∠ ABC = ∠ ABD, то прямая BC перейдет при этой симметрии в прямую BD. Ну, а поскольку BK = BL, то точка K при этой симметрии отображается в точку L. Но это и значит, что прямая KL перпендикулярна плоскости γ .
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1995 >> Районный тур >> 11 класс | Убрать решения |