Задача 1: Расставьте по кругу четыре единицы, три двойки и три тройки [три единицы, четыре двойки и три тройки] так, чтобы сумма любых трех подряд стоящих чисел не делилась на 3.

(С.~Берлов)

Решение: 1 вариант:

2 вариант:

Задача 2: Натуральное число можно умножать на два и произвольным образом переставлять в нем цифры (запрещается лишь ставить ноль на первое место). Докажите, что превратить число 1 в число 811 [411] с помощью таких операций невозможно.

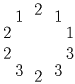
(А.~Голованов)

Решение: Ответ: нет.

Решение 1. Если бы из числа 1 можно было получить число 74 [78], то, выполняя операции перестановки цифр и деления четного числа на 2, из числа 74 [78] можно было бы получить 1. Попробуем: перестановка цифр приводит только к числу 47 [87], которое на два не делится, так что дальнейшие действия с ним не дадут ничего нового; деление числа 74 [78] на два дает нам число 37 [39], которое само нечетно, и полученное из него перестановкой цифр число 73 [93] тоже нечетно. Таким образом, попытка выполнить обратные преобразования приводит к получению всего трех новых чисел, среди которых нет единицы.

Решение 2. При выполнении операций количество цифр числа не уменьшается, поэтому если мы получили число, состоящее из трех или более цифр, то дальнейшие действия с ним никогда больше не приведут нас к двузначному числу. На схеме приведены все возможные способы применения операций, начинающиеся с числа 1 и до того момента, пока не получается трехзначное число. Как видим, число 74 [78] получить нельзя.

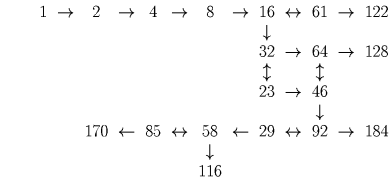
Решение 3 (для второго варианта): заметим, что указанные операции не могут из числа, не делящегося на 3, сделать число, на 3 делящееся.

Задача 3: На острове Невезения живут 100 [200] человек, причем некоторые из них всегда лгут, а остальные говорят только правду. Каждый житель острова поклоняется одному из трех богов – богу Солнца, богу Луны или богу Земли. Каждому жителю острова задали три вопроса:

1) Поклоняетесь ли Вы богу Солнца?

2) Поклоняетесь ли Вы богу Луны?

3) Поклоняетесь ли Вы богу Земли?

На первый вопрос утвердительно ответили 60 человек, на второй – 40 человек и на третий – 30 человек [110, 90, 60]. Сколько лжецов на острове?

(Ф.~Назаров)

Решение: Того, кто всегда говорит правду, будем называть рыцарем (такова традиция). Очевидно, что каждый рыцарь ответил утвердительно ровно на один вопрос, а каждый лжец – ровно на два вопроса. Поэтому суммарное количество утвердительных ответов – 130 – равно числу рыцарей плюс удвоенное число лжецов, т. е. всему населению острова плюс число лжецов. Так как всего на острове живет 100 человек, то количество лжецов – 30.

Во втором варианте решение совершенно аналогично. Ответ: 60.

Задача 4: Гриб называется плохим, если в нем больше 11 червяков. Червяк – тощий, если он съел не более 1/5 гриба, в котором живет. Четверть всех грибов в лесу плохие. Докажите, что не менее трети всех червяков – тощие.

[Гриб называется плохим, если в нем больше 15 червяков. Червяк – тощий, если он съел не более 1/7 гриба, в котором живет. Одна пятая часть всех грибов в лесу – плохие. Докажите, что не менее четверти всех червяков – тощие.]

(К.~Кохась, С.~Ягунов; )

Решение: Червяка, который съел больше 1/5 гриба, будем называть жирным. Ясно, что в любом грибе не более 4 жирных червяков. А так как в плохом грибе живет не меньше 12 червяков, то не меньше восьми из них – тощие. Пусть k – количество плохих грибов. Тогда тощих червяков в них не меньше, чем 8k, количество всех грибов в лесу – 4k, и количество жирных червяков не более 16k. Итак, тощих червяков не меньше, чем 8k, а нетощих – не больше, чем 16k, значит, тощих – не менее трети.

Во втором варианте решение аналогично: в каждом грибе живет не более 6 жирных, а в каждом плохом – не менее 10 тощих. Количество тощих червяков не меньше 10k, а количество жирных – не больше 6 • 5k, поэтому тощих червяков не менее четверти.