 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1998 >> Городской тур >> 8 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1998. Городской тур. 8 класс |
|
|
Найдите все такие пары натуральных чисел m и n, что
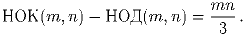
(А.~Голованов)
Задача 2:Точка D – середина стороны AC треугольника ABC. На стороне BC выбрана такая точка E, что ∠ BEA = ∠ CED. Найдите отношение длин AE:DE.
(С.Берлов)
Задача 3:Задача 4: Задача 5:
По кругу расставлены числа от 1 до 30. Стоящие на соседних местах числа можно поменять местами. После некоторого количества таких операций оказалось, что каждое число переместилось на диаметрально противоположное место. Докажите, что в некоторый момент меняли местами числа, сумма которых равна 31.
(С.Берлов)
Задача 6:Дана бесконечная последовательность натуральных чисел an, в которой при всех n выполняется соотношение an + 2 = НОД (an,an + 1) + 1\,. Может ли эта последовательность содержать более 1998 различных чисел?
(С.Берлов)
Задача 7:В оздоровительный лагерь приехало несколько школьников, каждый из которых имеет среди приехавших от 2 до 30 знакомых. Докажите, что опытный вожатый сможет расселить их в 60 комнат так, чтобы никакие два знакомых не оказались в одной комнате, и чтобы не было школьника, все знакомые которого живут в одной комнате.
(Д.~Карпов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1998 >> Городской тур >> 8 класс | Убрать решения |