 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1999 >> Городской тур >> 11 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1999. Городской тур. 11 класс |
|
|
Найдите наибольшее значение выражения
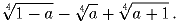
(А.~Голованов)
Задача 2:В последовательности натуральных чисел каждый член, начиная с третьего, равен либо сумме, либо модулю разности двух предыдущих. На доске выписаны первые 1999 членов этой последовательности. Докажите, что можно продолжить последовательность по этому правилу так, чтобы в ней снова встретились подряд эти 1999 чисел (в том же порядке).
(Д.~Ростовский)
Задача 3:Диагонали шестиугольного сечения куба пересекаются в одной точке. Докажите, что сечение проходит через центр куба.
(Р.~Исмаилов)
Задача 4:Вдоль прямого шоссе расставлены светофоры, на каждом попеременно минуту горит красный свет, минуту — зеленый (не обязательно синхронно). По шоссе со скоростью 60 км/ч едут в одном направлении две машины. На красный свет машина мгновенно останавливается, на зеленый — мгновенно возобновляет движение с той же скоростью. Докажите, что, если в начальный момент расстояние между машинами больше 2 км, то они никогда не встретятся.
(С.Берлов)
Задача 5: Задача 6:На клетках бесконечной доски стоят несколько шашек. Разрешается переместить любую шашку на клетку, симметричную ей относительно какой-нибудь другой шашки; допускается наличие нескольких шашек на одной клетке. В позициях A и B все шашки стоят на разных клетках, расположенных не на одной прямой, и из A можно получить B указанными операциями. Докажите, что это можно сделать так, чтобы и в промежуточных позициях все шашки стояли на разных клетках.
(К.~Кохась)
Задача 7:Докажите, что при k > 2 число 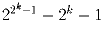 — составное.
— составное.
(Н.~Филонов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1999 >> Городской тур >> 11 класс | Убрать решения |