 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1999 >> Районный тур >> 10 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1999. Районный тур. 10 класс |
|
|
Задача 2:
Можно ли расставить в клетках таблицы 3 × 3 девять различных двузначных чисел так, чтобы произведение чисел в любых двух соседних клетках делилось на 2520? (Клетки считаются соседними, если они имеют общую сторону.)
(К. Кохась)
Задача 3:AL и BM — биссектрисы треугольника ABC. Известно, что одна из точек пересечения описанных окружностей треугольников ACL и BCM лежит на отрезке AB. Докажите, что ∠ ACB = 60.
(Е.Сопкина)
Задача 4:Найдите все тройки неотрицательных чисел x,y,z, удовлетворяющих системе уравнений
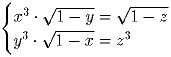
(С.~Иванов, С.~Берлов)
Задача 5:Числа от 1 до 600 выписаны в строчку в таком порядке, что при вычеркивании всех чисел, больших 300, остается возрастающая последовательность, а при вычеркивании всех чисел, не превосходящих 300, остается убывающая последовательность. Докажите, что сумма чисел, расположенных на местах со 151-го по 450-е, делится на 3.
(С.~Иванов, С.~Берлов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1999 >> Районный тур >> 10 класс | Убрать решения |