 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Городской тур >> 11 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2000. Городской тур. 11 класс |
|
|
Равносторонний треугольник со стороной 9 разбит на 81 равных треугольников отрезками, параллельными сторонам. Докажите, что из него нельзя вырезать более 18 параллелограммов со сторонами 1 и 2.
(О.Ванюшина)
Задача 2:Точка O — начало координат в трехмерном пространстве. Точки A1, A2, …, An имеют неотрицательные координаты. Докажите неравенство
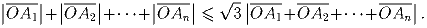
(А.~Храбров)
Задача 3:Каждый месяц лесник Ермолай сажал вдоль забора ряд из 2000 деревьев. К каждому дереву он прибивал табличку, на которой указывал сколько дубов есть среди самого дерева, его левого и правого соседей. Таким образом получалась последовательность из 2000 чисел. Сколько различных последовательностей мог получить лесник Ермолай?
(А.~Храбров, Д.~Ростовский)
Задача 4:Дан многочлен F(x) = x²ººº – x¹ººº + 1. Докажите, что не существует
8002 различных натуральных чисел a1, a2, …, a8002 таких, что
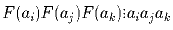 при всех попарно различных
i, j и k?
при всех попарно различных
i, j и k?
(А.~Баранов)
Задача 5:В остроугольном треугольнике ABC проведены высоты AA1, BB1, CC1. На стороне BC взята точка K, для которой ∠ BB1K = ∠ A, а на стороне AB точка M, для которой ∠ BB1M = ∠ C, L — точка пересечения высоты BB1 и отрезка A1C1. Докажите, что четырехугольник B1KLM — описанный.
(А.~Храбров, Д.~Ростовский)
Задача 6:Какое наибольшее число ладей можно расставить на шахматной доске n × n так, чтобы каждая из них била четное число других? Мы считаем, что одна ладья бьет другую, если они стоят на одной вертикали или горизонтали и между ними нет других ладей.
(Д.~Карпов)
Задача 7:Про иррациональные положительные числа α , β , γ и δ известно, что при любом натуральном n имеет место тождество [n α ] • [n β ] = [n γ ] • [n δ ]. Следует ли отсюда, что множества α , β и γ , δ совпадают? (Квадратные скобки, как обычно, обозначают целую часть числа).
(А.~Храбров)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Городской тур >> 11 класс | Убрать решения |