 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Городской тур >> 9 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2000. Городской тур. 9 класс |
|
|
С двух сторон дороги посадили два ряда по 1000 деревьев. На каждое дерево прибили табличку, в которой указано, сколько дубов среди этого дерева и его соседей слева и справа (у крайних деревьев — среди самого дерева и его единственного соседа). Оказалось, что две последовательности чисел на табличках совпадают. Докажите, что в обоих рядах дубы растут на одних и тех же местах.
(Д.~Ростовский, А.~Храбров)
Задача 2:В остроугольном треугольнике ABC проведены высоты AA1 и CC1. На высоте AA1 выбрана точка D такая, что A1D = C1D. Точка E — середина стороны AC. Докажите, что точки A, C1, D и E лежат на одной окружности.
(С.~Берлов)
Задача 3:F(x) = x²ººº – x¹ººº + 1. Существуют ли такие различные натуральные числа a1, a2, …, a2001, что F(ai)F(aj) делится на aiaj при всех i ≠ j?
(А.~Баранов)
Задача 4:На координатной плоскости проведена 101 прямая и отмечены все точки их пересечения друг с другом. Может ли быть так, что на каждой из проведенных прямых лежат 50 отмеченных точек с положительными первыми координатами и 50 — с отрицательными?
(С.Иванов)
Задача 5:На доске написаны натуральные числа 1, 2, …, 2000. Два игрока поочередно делают ходы по следующим правилам. Разрешается стереть любые два числа a и b и написать вместо них ab. Через некоторое время на доске останется одно число. Первый игрок выигрывает, если оно оканчивается на 2, 7 или 8, а второй — в противном случае. Кто выиграет при правильной игре?
(В.~Франк)
Задача 6:Вневписанная окружность треугольника ABC касается его стороны BC в точке K, а продолжения стороны AB — в точке L. Другая вневписанная окружность касается продолжений сторон AB и BC в точках M и N соответственно. Прямые KL и MN пересекаются в точке X. Докажите, что CX — биссектриса угла ACN.
(С.~Берлов)
Задача 7:Сложностью последовательности a1, a2, …,
составленной из нулей и единиц, называется наименьшее натуральное число k
такое, что для некоторых натуральных чисел 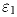 ,
, 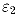 ,
…,
,
…, 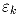 каждый член последовательности an, n > k,
имеет ту же четность, что и
каждый член последовательности an, n > k,
имеет ту же четность, что и
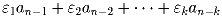 .
Последовательность a1, a2, … имеет
сложность 1000. Какова может быть сложность последовательности 1 – a1,
1 – a2, …? (Укажите все возможные значения и докажите, что других нет).
.
Последовательность a1, a2, … имеет
сложность 1000. Какова может быть сложность последовательности 1 – a1,
1 – a2, …? (Укажите все возможные значения и докажите, что других нет).
(А.~Кириченко)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Городской тур >> 9 класс | Убрать решения |