Задача 1:

a и b — положительные числа. Сумма минимального значения квадратного трехчлена f(x) = ax² + 8x + b и минимального значения трехчлена g(x) = bx² + 8x + a равна нулю. Докажите, что эти минимальные значения оба равны нулю.

(А.~Храбров)

Задача 2:

Задача 3:

В трапеции ABCD с основаниями AD и BC угол A — прямой, E — точка пересечения диагоналей, точка F — проекция E на сторону AB. Докажите, что углы DFE и CFE равны.

(С.~Берлов)

Задача 4:

Задача 5:

Последовательность вещественных чисел x₁, x₂,…удовлетворяет равенству

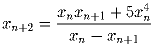
при всех натуральных n. При этом x₂₀₀₀ = x₁. Докажите, что x₁₉₉₉ ≠ x₂.

(С.Иванов)