 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Районный тур >> 11 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2000. Районный тур. 11 класс |
|
|
Дима сложил из одинаковых кубиков прямоугольный параллелепипед (ребра кубиков равны 1), написал на бумажке числа 42, 48 и 82 и сказал, что это — объём, площадь поверхности и сумма длин всех ребер этого параллелепипеда, но не сказал, где какое число. Чему равны длины ребер диминого параллелепипеда?
(О.Ванюшина)
Задача 2:Отрезки AM и BH — соответственно медиана и высота остроугольного треугольника ABC. Известно, что AH = 1 и 2 ∠ MAC = ∠ MCA. Найдите длину стороны BC.
(Ф.~Бахарев)
Задача 3:В соревнованиях по художественному скалолазанию каждая участница набрала целое число баллов. Известно, что победительница набрала ровно в 4 раза меньше баллов, чем все остальные участницы вместе взятые, скалолазка, занявшая третье место, набрала ровно в 9 раз меньше баллов, чем все остальные, а скалолазка, занявшая последнее место, набрала ровно в 10 раз меньше, чем все остальные. Сколько скалолазок участвовало в соревнованиях?
(С.~Берлов, С.~Иванов)
Задача 4:Функция f задана при всех вещественных x и для любого x удовлетворяет неравенствам:
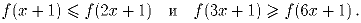
(А.~Храбров)
Задача 5:В таблице 3 × 3 разрешается выбрать любую строку или столбец и домножить все числа, стоящие в выбранной строке (столбце), на произвольное положительное вещественное число. Может ли в результате применения нескольких таких операций из левой таблицы получиться правая?

(А.~Храбров)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Районный тур >> 11 класс | Убрать решения |