 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Районный тур >> 9 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2000. Районный тур. 9 класс |
|
|
В прямоугольном треугольнике ABC с прямым углом B провели медиану BM. K и L — точки касания вписанной окружности треугольника ABM со сторонами AB и AM. Известно, что прямые KL и BM параллельны. Найдите угол ACB.
(Р.Исмаилов)
Задача 3:В чемпионате по рыбной ловле участвовало несколько рыбаков. Известно, что победитель (поймавший наибольшее число рыб) поймал ровно в 4 раза меньше рыб, чем все остальные участники вместе взятые. Рыбак, занявший третье место, поймал ровно в 9 раз меньше, чем все остальные, а рыбак, оказавшийся на последнем месте, поймал ровно в 10 раз меньше, чем все остальные. Сколько рыбаков участвовало в соревновании?
(С.~Берлов, С.~Иванов)
Задача 4: Задача 5:Числа a, b, c, d лежат в промежутке от 2 до 4. Докажите неравенство:
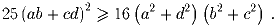
(А.~Храбров)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2000 >> Районный тур >> 9 класс | Убрать решения |