 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 11 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2001. Городской тур. 11 класс |
|
|
Существуют ли такие различные числа x, y, z из [0, π /2], что шесть чисел sin x, sin y, sin z, cos x, cos y и cos z можно разбить на три двойки с равными суммами.
Задача 2:В стране 2000 городов и полностью отсутствуют дороги. Докажите, что можно соединить дорогами некоторые города так, чтобы из двух городов выходило по одной дороге, из двух — по две дороги, из двух — по три, …, из двух — по 1000 дорог.
(Ф.Бахарев)
Задача 3:Точки A1, B1 и C1 — середины сторон BC, CA и AB треугольника ABC. На средних линиях C1B1 и A1B1 отмечены точки E и F так, что прямая BE содержит биссектрису угла AEB1, а пряма BF — биссектрису угла CFB1. Докажите, что углы BAE и BCF равны.
(Ф.Бахарев)
Задача 4:Для любых натуральных чисел n > m докажите неравенство
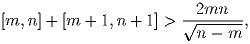
(А.Голованов)
Задача 5:Точка I — центр окружности, вписанной в остроугольный треугольник ABC, а точка H — ортоцентр этого треугольника. Точка M — середина меньшей дуги AC описанной окружности треугольника ABC. Оказалось, что MI = MH. Найдите угол ∠ ABC.
(Ф.Бахарев)
Задача 6:Найдите все такие функции 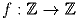 , что для любых целых x и y
выполняется соотношение f(x + y + f(y)) = f(x) + 2y.
, что для любых целых x и y
выполняется соотношение f(x + y + f(y)) = f(x) + 2y.
(Ф.Петров)
Задача 7:Из таблицы 20 × 20 вырезали прямоугольники 1 × 20, 1 × 19, …, 1 × 1. Докажите, что наибольшее количество прямоугольников 1 × 2, которое заведомо можно вырезать из оставшейс части таблицы равно 85.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 11 класс | Убрать решения |