Задача 1:
Задача 2:
Костя задумал натуральное число, перемножил все его цифры и результат умножил
на задуманное число. Получилось 1716. Какое число задумал Костя?
Найдите все возможные ответы и докажите, что других ответов нет.
Решение:
Пусть Костя задумал число x.
В разложении 1716 = 2 • 2 • 3 • 11 • 13
есть множители 11 и 13. Эти множители не могли быть
появиться от перемножения цифр, значит x делится на 11 • 13 = 143.
Само число 143 подходит.
Теперь достаточно лишь проверить числа 2 • 143 = 286,
3 • 143 = 429, 2 • 2 • 143 = 572 и 2 • 3 • 143 = 858.
Других ответов среди них нет.
Ответ: 143.
Задача 3:
Дети гуляют во дворе детского сада. Тех из них, у кого на ногах надето
поровну носков, в 5 раз меньше, чем тех, у кого не поровну. Воспитательница
велела детям переодеться, и каждый ребенок снял с одной ноги носок и надел
его на другую ногу. Теперь тех, у кого носков на ногах поровну, стало в 2
раза меньше, чем тех, у кого не поровну. Могло ли быть так, что в начале
прогулки более чем у половины детей на одной ноге было ровно на один носок
меньше, чем на другой?
У тех, у кого носков было поровну
(их была 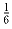 часть), станет не поровну.
Кроме того, у тех, у кого на одной ноге было ровно на один носок меньше, чем на другой,
после переодевания также тоже будет не поровну носков.
Поэтому, если их больше половины, то более чем у
часть), станет не поровну.
Кроме того, у тех, у кого на одной ноге было ровно на один носок меньше, чем на другой,
после переодевания также тоже будет не поровну носков.
Поэтому, если их больше половины, то более чем у
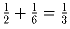 будет не поровну носков.
будет не поровну носков.
(К. Кохась)
Задача 4:
Вдоль правой стороны дороги припарковано 100 машин. Среди них —
30 красных, 20 желтых и 20 розовых мерседесов. Известно, что
никакие два мерседеса разного цвета не стоят рядом. Докажите, что тогда
какие-то три мерседеса, стоящие подряд, — одного цвета.
(К. Кохась)
Решение:
Фраза «никакие два мерседеса разного цвета не стоят рядом»
означает, что рядом могут стоять только одноцветные мерседесы.
Разобьём машины на 33 тройки, стоящих подряд
(при этом одна машина останется). Поскольку машин, не являющихся мерседесами,
всего 100 – 30 – 20 – 20 = 30 штук, то в какой-то тройке все три машины – мерседесы,
а значит они все одного цвета.


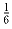 часть), станет не поровну.
Кроме того, у тех, у кого на одной ноге было ровно на один носок меньше, чем на другой,
после переодевания также тоже будет не поровну носков.
Поэтому, если их больше половины, то более чем у
часть), станет не поровну.
Кроме того, у тех, у кого на одной ноге было ровно на один носок меньше, чем на другой,
после переодевания также тоже будет не поровну носков.
Поэтому, если их больше половины, то более чем у
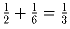 будет не поровну носков.
будет не поровну носков.