Задача 1: Действительные числа a, b, c, x, y, z удовлетворяют неравенствам: a² + b² + c² ≤ 6 и x² + y² + z² ≤ 24. Докажите, что

a) ax + by + cz ≤ 15

b) ax + by + cz ≤ 12.

Решение: Докажем сразу пункт б).

1 решение. Рассмотрим в пространстве точки M(a,b,c) и N(x,y,z). Тогда условия задачи запишутся в виде: . Имеем: где  α  – угол между векторам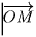и и .

2 решение. Запишем второе неравенство в виде 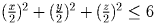и сложим его с первым. В силу неравенства между средним арифметическим и средним геометрическим, . Аналогично, и что завершает доказательство.

Задача 2: На плоскости задано 2N точек. Два игрока играют в следующую игру: каждый из них в свою очередь хода выбирает точку из числа еще не выбранных. После того, как все точки разобраны, каждый из игроков подсчитывает сумму попарных расстояний между N выбранными им точками. Побеждает тот игрок, у которого эта сумма меньше. Докажите, что при правильной игре начинающий не проиграет.

Решение:

Назовем весом точки A (w(A)) сумму расстояний от нее до остальных отмеченных точек. Стратегия начинающего: очередным ходом он выбирает точку с наименьшим весом. Покажем, что эта стратегия искомая. Пусть начинающий, играя согласно стратегии, выбрал последовательно точки A₁, A₃,  … , A_2N – 1, а его оппонент – точки A₂, A₄,  … , A_2N. Тогда w(A₁) ≤ w(A₂) w(A₃) ≤ w(A₄),  … , w(A_2N – 1) ≤ w(A_2N), поэтому сумма весов точек, выбранных начинающим – (S₁), меньше соответствующей суммы его противника – S₂. Заметим, что каждое расстояние между точками, номера которых разнолй четности, войдет по одному разу и в S₁ и в S₂, расстояние между точками с четными номерами – дважды в S₂, а с нечетными – дважды в S₁. Но тогда сумма расстояний между точками с нечетными номерами не больше суммы расстояний между точками с четными номерами, поэтому начинающий не проиграл. Утверждение доказано.

Задача 3: Kаждая сторона треугольника разделена на 3 равные части, и проведены прямые, как указано на рисунке. Во сколько раз площадь заштрихованного треугольника меньше площади исходного?

Решение: Пусть S – площадь исходного треугольника, S₁ – площадь незаштрихованной части. Тогда S₁ равна сумме площадей треугольников ABM, BPC и ACN минус сумма площадей трех примыкающих к углам маленьких тругольников. Выразим через S площадь каждого такого треугольника, для чего проведем через точку N прямую, параллельную прямой BM (см. рис.9). Пусть K – точка пересечения этой прямой со стороной AC. Из подобия треугольников CNK и CBM имеем: CK:CM = CN:CB = ⅓, поэтому 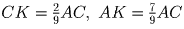. Из подобия треугольников ATM и ANK получаем: . Тогда, так как S_ABM = S_BPC = S_ANC = ⅓S, имеем: . Аналогично, площадь каждого из примыкающих к углам треугольничков равна 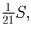поэтому 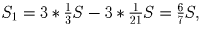следовательно отношение площади треугольника ABC к площади заштрихованного равно 7.

Ответ: в семь раз.

Задача 4: Вася выписывает в тетрадку натуральные числа N₁, N₂,  … ,  N_k, N_k + 1,  …  по следующему правилу: N₁ выбирается произвольно, а N_i + 1 равно увеличенному на 3000 остатку от деления числа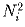 на 1996. Докажите, что всегда найдется бесконечное множество равных между собой чисел номера которых образуют возрастающую арифметическую прогрессию.

Решение: Все числа N_i, начиная со второго, натуральные и лежат в отрезке [3000;4995], поэтому различных чисел среди них не более 1996, значит, среди чисел N₂, N₃,  … , N₁₉₉₈ обязательно найдутся два одинаковых, скажем, 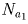и 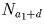. Так как каждое число однозначно определяется предыдущим, имеем: 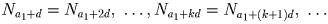. Числа – искомые.