Задача 1:
Докажите, что для любых положительных чисел x, y, и z
выполняется неравенство:
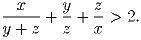
Решение:
Умножим неравенство на положительное число xz(y + z) и
получим квадратное неравенство относительно x: zx² + x(y² – yz – 2z²) + z²(y + z) ≥ 0. Дискриминант квадратного
трехчлена в левой части равен
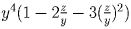
.
Если
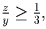
то он неположителен,
а коэффициент при x² положителен, поэтому неравенство верно для
любого x. Пусть
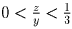
. Тогда квадратный
трехчлен имеет два корня одного знака (так как его свободный член
положителен). Однако в этом случае y² – yz – 2z² > 4z² > 0,
то есть сумма корней отрицательна, значит оба корня отрицательны
и при всех положительных x трехчлен положителен, что и завершает
доказательство.
Задача 2:
Дан треугольник ABC, в котором AB = BC. На стороне AB выбрана
точка E, а на продолжении стороны AC за точку A – точка D
так, что ∠ BDC = ∠ ECA. Докажите, что площади треугольников
DEC и ABC равны.
Решение:
Заметим, что треугольники DBC и ECA подобны по 2 углам
( ∠ BDC = ∠ ECA по условию, а ∠ BCD = ∠ EAC
как углы при основании равнобедренного треугольника – см.рис.11.).
Так как в подобных треугольниках высоты относятся так же, как и
стороны, на которые они опущены, имеем:
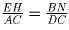
.
Тогда S
ABC = ½*AC*BN = ½*EH*DC = S
DEC,
что и требовалось доказать.
Задача 3:
Найдите все натуральные числа n, при которых дробь
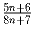
сократима.
Решение:
Пусть p – натуральное число, на которое сократима данная дробь
(p ≠ 1). Тогда 5n + 6 = α p, 8n + 7 = β p. Ввиду очевидного
равенства p(8 α – 5 β ) = 8(5n + 6) – 5(8n + 7) = 13, число p –
отличный от 1 делитель числа 13, а значит p = 13. Имеем 5n + 6 = 13 α ,
для некоторого натурального α . Переписав это равенство в виде
5(n + 9) = 13( α – 3), видим, что n + 9 делится на 13, т.е.
n = 13m – 9, где m – натуральное. Непосредственной проверкой
убеждаемся, что все такие n удовлетворяют условию задачи.
Задача 4:
В так-тиль играют вдвоем на
доске 4 × 4 восемью шашками двух
цветов. Начальное расположение шашек указано на рисунке. Игроки ходят
по очереди, начинают игру белые. Ход заключается в перестановке шашки
своего цвета на соседнее по вертикали или по горизонтали (но
не по диагонали) свободное поле.
Побеждает игрок, первым выстроивший ряд из
трех своих шашек (по горизонтали, вертикали или диагонали). Двое
школьников не успели доиграть на уроке партию и отложили ее.
Вернувшись с перемены, они напрочь забыли, чей ход в отложенной
позиции. Всегда ли они смогут восстановить очередность хода?
Решение:
Ответ: да, всегда. Раскрасим доску для игры в так-тиль в шахматном порядке
(см. рис.12). Тогда в начальной позиции все шашки стоят на полях
своего цвета, а каждый ход любого из игроков меняет цвет поля
ровно одной шашки, поэтому число шашек, стоящих на полях
своего цвета, будет нечетным после каждого хода белых и четным
после каждого хода черных. Вывод: по позиции всегда можно
установить очередность хода.


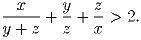
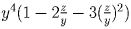 .
Если
.
Если 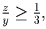 то он неположителен,
а коэффициент при x² положителен, поэтому неравенство верно для
любого x. Пусть
то он неположителен,
а коэффициент при x² положителен, поэтому неравенство верно для
любого x. Пусть 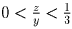 . Тогда квадратный
трехчлен имеет два корня одного знака (так как его свободный член
положителен). Однако в этом случае y² – yz – 2z² > 4z² > 0,
то есть сумма корней отрицательна, значит оба корня отрицательны
и при всех положительных x трехчлен положителен, что и завершает
доказательство.
Задача 2:
Дан треугольник ABC, в котором AB = BC. На стороне AB выбрана
точка E, а на продолжении стороны AC за точку A – точка D
так, что ∠ BDC = ∠ ECA. Докажите, что площади треугольников
DEC и ABC равны.
. Тогда квадратный
трехчлен имеет два корня одного знака (так как его свободный член
положителен). Однако в этом случае y² – yz – 2z² > 4z² > 0,
то есть сумма корней отрицательна, значит оба корня отрицательны
и при всех положительных x трехчлен положителен, что и завершает
доказательство.
Задача 2:
Дан треугольник ABC, в котором AB = BC. На стороне AB выбрана
точка E, а на продолжении стороны AC за точку A – точка D
так, что ∠ BDC = ∠ ECA. Докажите, что площади треугольников
DEC и ABC равны.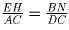 .
Тогда SABC = ½*AC*BN = ½*EH*DC = SDEC,
что и требовалось доказать.
Задача 3:
Найдите все натуральные числа n, при которых дробь
.
Тогда SABC = ½*AC*BN = ½*EH*DC = SDEC,
что и требовалось доказать.
Задача 3:
Найдите все натуральные числа n, при которых дробь 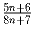 сократима.
сократима.