Задача 1: 1995-значное число заканчивается на 1, и всякое двузначное число, образованное его соседними цифрами, идущими в том же порядке, делится либо на 17, либо на 23. Какова первая цифра этого числа? Делится ли оно на 3? На 9?

Решение:

Пусть данное число имеет вид: 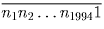. Выпишем все двузначные числа, делящиеся на 17 или на 23 – 51,92,23,34,85,46,17, 68,69, и заметим, что последняя цифра этих чисел однозначно определяет само число. Тогда так как 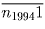делится либо на 17, либо на 23 n₁₉₉₄ = 5. Аналогично, n₁₉₉₃ = 8, n₁₉₉₂ = 6, и.т.д. Таким образом, данное число имеет вид: 4692346 … 92346851, а его первая цифра – 4. Подсчитаем сумму цифр числа: 10 + 24*399 + 14 = 9600. Следовательно, оно делится на 3, и не делится на 9.

Задача 2: Для всех значений a, b и c решить систему:

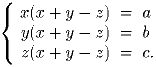
Решение:

Сложив первое уравнение со вторым и вычтя третье, получаем: (x + y – z)² = a + b – c. Если a + b – c < 0, то решений нет. Пусть a + b – c = 0. Тогда x + y – z = 0, следовательно a = b = c = 0. Наконец, если a + b – c > 0, то .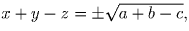

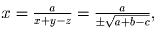
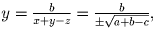
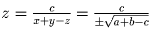Ответ: если a + b – c < 0, или a + b – c = 0, но хотя бы одно из чисел a, b или c отлично от 0, то решений нет. Если a = b = c = 0, то решений бесконечно много: все тройки чисел x, y, z, удовлетворяющие уравнению x + y – z = 0. Если a + b – c > 0, то решений два: , , .

Задача 3: На плоскости дан выпуклый многоугольник. Из середины каждой его стороны перпендикулярно к ней выходит вектор, направленный наружу многоугольника и равный по длине половине стороны из которой он выходит. Докажите, что сумма всех таких векторов равна нулю.

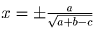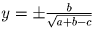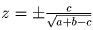Решение: Пусть дан многоугольник A₁A₂ … A_n. Повернем все векторы на 90° по часовой стрелке. Тогда вектор их суммы также окажется повернут на 90° по часовой стрелке. С другой стороны, вектор, выходящий из стороны A_iA_i + 1 многоугольника, перейдет в вектор 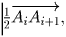а сумма всех таких векторов равна .

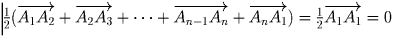Задача 4: На плоскости проведено семь прямых, никакие две из которых не параллельны. Докажите, что из них можно выбрать две, угол между которыми не превосходит 26°.

Решение:

Без ограничения общности полагаем, что все прямые проходят через одну точку. Эти прямые разбивают плоскость на 14 углов. Так как 360:14 < 26, среди этих углов есть угол, не превосходящий 26°. Прямые, являющиеся его сторонами – искомые.