 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Районный тур >> 11 класс | Убрать решения |
|
|
| XXXVI Екатеринбургская городская олимпиада, 1995-1996. Районный тур. 11 класс |
|
|
Решение:
Ответ: для всех четных N. В самом деле, если N четно, достаточно N шагов: на i-м шаге переворачиваем все пятаки, кроме i-го. Если же N нечетно, то число пятаков, лежащих гербами вверх, все время остается нечетным, поэтому отличным от нуля.
Задача 2: Можно ли в таблицу N × (N – 1) вписать натуральные числа так, чтобы сумма чисел в каждой строке имела вид
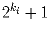 , а в каждом
столбце – 14mj + 5, где ki и mj – некоторые натуральные
числа.
, а в каждом
столбце – 14mj + 5, где ki и mj – некоторые натуральные
числа.Решение:
Нет, нельзя. Действительно, предположим, что можно, и пусть
сумма чисел в i-ой строке равна 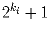 , а в j-м
столбце – 14mj + 5, где ki и mj – некоторые
натуральные числа. Пусть S – сумма чисел во всей таблице. Тогда с
одной стороны,
, а в j-м
столбце – 14mj + 5, где ki и mj – некоторые
натуральные числа. Пусть S – сумма чисел во всей таблице. Тогда с
одной стороны,
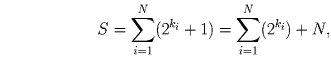
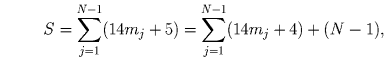
Решение:
Данное неравенство равносильно совокупности систем
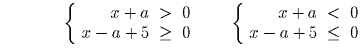
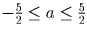 так как a – 5 ≤ – a ≤ a + 5,
любое x ≠ – a хотя бы одной из систем удовлетворяет.
Если
так как a – 5 ≤ – a ≤ a + 5,
любое x ≠ – a хотя бы одной из систем удовлетворяет.
Если 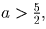 то
то 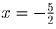 не удовлетворяет
ни одной из систем.
При
не удовлетворяет
ни одной из систем.
При 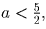 таким числом будет
таким числом будет 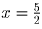 .
.Ответ: 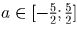 .
.
Решение: Без ограничения общности, пусть разрезаемый квадрат единичный. Пусть также ai и bi меньшая и большая сторона i-го прямоугольника, а всего прямоугольников – N. Утверждение задачи следует тогда из цепочки неравенств:
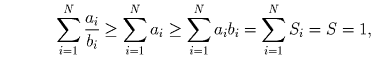
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Районный тур >> 11 класс | Убрать решения |