Задача 1: Существуют ли три последовательных натуральных числа, каждое из которых делится на квадрат какого-либо целого числа, отличного от 1?

Решение:

Да, существуют. Например: 48 = 4² • 3, 49 = 7², 50 = 5² • 2.

Задача 2: На школьной викторине было предложено 33 вопроса. За каждый правильный ответ ученику засчитывали 7 очков, а за неправильный с него списывали 12 очков. На сколько вопросов отвечал ученик и сколько верных ответов он дал, если он набрал 77 очков и известно, что по крайней мере один раз ученик ошибся?

Решение:

Пусть ученик дал x верных ответов и y раз ошибся. Учитывая, что число вопросов не более 33, имеем систему:

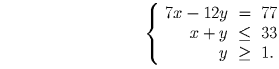
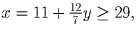Из первого уравнения следует, что y делится на 7. При y ≥ 10 имеем что противоречит второму неравенству системы. Поэтому y = 7, x = 23, а число вопросов, на которые отвечал ученик – 30.

Задача 3: Можно ли расположить на плоскости 6 точек так, чтобы среди любых 3-х из них нашлись две, расстояние между которыми в точности равно 1 м.?

Решение: Да, можно. Достаточно расположить их в вершинах 2-х равносторонних треугольников со стороной 1 м каждый.

Задача 4: Наименьшая из сторон треугольника ABC больше наибольшей стороны треугольника EFG. Верно ли, что площадь треугольника ABC обязательно больше площади треугольника EFG?

Решение:

Нет, неверно. Пример: треугольник EFG равносторонний со стороной 1, а треугольник ABC равнобедренный с основанием 10 и высотой 0,01.