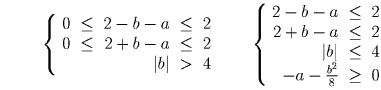Задача 1:
Найти все пары a и b, для которых неравенство
( cos 2x – a – b cos x)² ≤ 1
выполнено для всех x.
Решение: Обозначим t = cos x. Тогда условие задачи будет выглядеть
следующим образом: найти все пары чисел a и b при которых
для всех t ∈ [0;1] справедливо неравенство:
|2t² – 1 – a – bt| ≤ 2. Пусть f(t) = 2t² – a – bt.
График f(t) – парабола с ветвями, направленными вверх и с
вершиной в точке 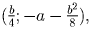 поэтому
наибольшее значение f(t) достигается на одном из концов
отрезка, а наименьшее – либо тоже на одном из концов (при
|b| > 4), либо в точке
поэтому
наибольшее значение f(t) достигается на одном из концов
отрезка, а наименьшее – либо тоже на одном из концов (при
|b| > 4), либо в точке 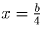 (в противном
случае). Имеем совокупность систем:
(в противном
случае). Имеем совокупность систем:
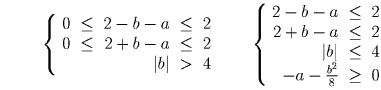
Изобразив соответствующие множества на плоскости XOY,
убеждаемся, что первая система решений не имеет, а вторая имеет
единственное решение a = b = 0.
ОТВЕТ: при a = b = 0.
Задача 2:
С помощью циркуля и линейки построить треугольник ABC
по стороне AB, углу C и сумме сторон AC + BC.
Решение:
Напомним, что множество точек плоскости, из которых
отрезок AB виден под углом α , есть объединение двух
дуг окружностей (см. рисунок).
Пусть задача решена. Продолжим сторону BC и отложим на ней отрезок
CC1 = CA. Так как треугольник ACC1 равнобедренный,
Задача 3:
Докажите, что многочлен x
3m + x
3n + 1 + x
3p + 2
делится на x² + x + 1 при любых натуральных числах m, n и p.
Задача 4:
N кубов в пространстве расположены так, что все их ребра
параллельны осям координат, и любые два куба имеют общую точку.
Докажите, что пересечение всех кубов непусто.


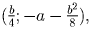 поэтому
наибольшее значение f(t) достигается на одном из концов
отрезка, а наименьшее – либо тоже на одном из концов (при
|b| > 4), либо в точке
поэтому
наибольшее значение f(t) достигается на одном из концов
отрезка, а наименьшее – либо тоже на одном из концов (при
|b| > 4), либо в точке 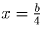 (в противном
случае). Имеем совокупность систем:
(в противном
случае). Имеем совокупность систем: