Задача 1: Доказать неравенство:

Решение:

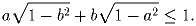
В силу неравенства между средним арифметическим и средним геометрическим имеем: 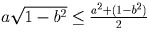и 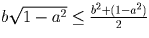. Сложив полученные неравенства, получим требуемое.

Задача 2: На стороне AC треугольника ABC найти точку M, такую что отрезки прямых, проходящих через M параллельно сторонам AB и BC, заключенные между сторонами треугольника, были равны.

Решение:

По условию задачи четырехугольник PMQB обязан быть ромбом (см. рисунок). Но тогда его диагональ BM является биссектрисой угла B. Значит, M – основание биссектрисы угла B треугольника ABC.

Задача 3: Сколько решений в целых числах имеет уравнение: x² = y² + pq, где p и q – простые числа?

Решение:

По условию pq = x² – y² = (x – y)(x + y). Заметим, что x – y и x + y имеют одинаковую четность, значит pq либо делится на 4, либо нечетно. Первый случай возможен лишь при p = q = 2. Тогда x – y =  ± 2, x + y =  ± 2, откуда y = 0, x =  ± 2. Пусть pq нечетно. При p ≠ q оно имеет 8 различных делителей ( ± 1,  ± p,  ± q,  ± pq), при p = q – 6 ( ± 1,  ± p,  ± p²). Число x – y может быть любым из них, и так как все эти делители нечетны, числа x и y всегда окажутся целыми.

ОТВЕТ: 6 решений, если p = q ≠ 2, 2 решения, если p = q = 2, нет решений, если p ≠ q и p или q равно 2, и 8 решений если p ≠ q и p и q – нечетны.

Задача 4: В жюри олимпиады входят 8 человек. Их суммарный возраст – 280 лет. Докажите, что из них можно выбрать троих, сумма возрастов которых не менее 105 лет.

Решение: Рассмотрим трех самых старших членов жюри. Если их суммарный возраст менее 105 лет, то среди них есть член жюри моложе 35 лет, Но тогда каждому из остльных пяти членов жюри также меньше 35 лет, и суммарный возраст членов жюри строго меньше 105 + 35*5 = 280 лет, что противоречит условию.