 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Заочный тур >> 9 класс | Убрать решения |
|
|
| XXXVI Екатеринбургская городская олимпиада, 1995-1996. Заочный тур. 9 класс |
|
|
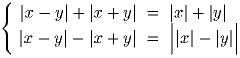
Решение: Возведя оба уравнения в квадрат и почленно их сложив, получим: 2x² + 2y² = 0, откуда x = y = 0. Проверка показывает, что данная пара действительно является решением. Задача 2: Точка F – середина боковой стороны трапеции ABCD. Найдите отношение площади треугольника CFD к площади всей трапеции ABCD.
Решение:
Пусть высота трапеции h. В зависимости от обозначений
возможны три случая (см. рисунок). В случае, изображенном на
рис. a, треугольник
CFD вырожденный, и искомое отношение равно 0.
Если имеет место рис.b, то 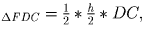 а
а 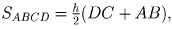 поэтому
искомое отношение равно
поэтому
искомое отношение равно 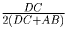 и может принимать
любое значение от 0 (при неограниченно большом AB) до ½
(при AB стремящимся к нулю). Наконец, в последнем случае проведем
FL – среднюю линию трапеции (см. рис. c).
Тогда
и может принимать
любое значение от 0 (при неограниченно большом AB) до ½
(при AB стремящимся к нулю). Наконец, в последнем случае проведем
FL – среднюю линию трапеции (см. рис. c).
Тогда 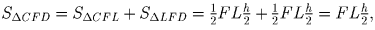 а
а 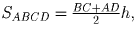 откуда искомое отношение равно ½.
откуда искомое отношение равно ½.
ОТВЕТ: любое число из отрезка [0;½].
Задача 3: Докажите, что уравнение y² = 5x² + 6 не имеет решений в целых числах.Решение:
Eсли x делится на 3, то y также должно делится на 3, тогда 6 = y² – 5x² делится на 9 – противоречие. Если же x = 3m ± 1, то x² при делении на 3 дает в остатке 1, тогда 5x² + 6 при делении на 3 дает в остатке 2, поэтому не может являться квадратом целого числа.
Задача 4: Плоскость раскрашена a) в 2; b) в 3; c) в 100 цветов. Докажите, что на плоскости существует прямоугольник, все вершины которого окрашены в один и тот же цвет.Решение:
Докажем сразу пункт с).
Назовем i-м столбцом (i натуральное число) множество точек плоскости с координатами (i,n), где n ≤ 101 и n – натуральное. 101 точку можно раскрасить в 100 цветов ровно 100¹º¹ различным способом, поэтому среди первых 100¹º¹ + 1 столбцов найдутся два (скажем, i1 и i2) раскрашенных одинаково столбца. Но среди 101 точки i1-го найдутся две окрашенных в один цвет. Пусть их ординаты n1 и n2. Тогда точки (i1,n1), (i1,n2), (i2,n2), и (i2,n1) окрашены в один цвет и, очевидно, являются вершинами прямоугольника.
Примечание: как видно из доказательства, утверждение справедливо для любого числа цветов.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Заочный тур >> 9 класс | Убрать решения |