 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 11 класс >> 1-й день | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 11 класс. 1-й день |
|
|
Докажите, что для любого натурального числа n справедливо двойное неравенство:
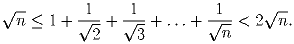
(Предложена С.А.Аникиным.)
Решение: Так как слагаемых n и каждое из них больше или равно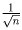 , то
, то
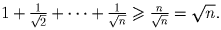 Оценка сверху получается индукцией по n.
Действительно, при n = 1 неравенство справедливо.
Допустим, что оно справедливо при n = k + 1.
Тогда
Оценка сверху получается индукцией по n.
Действительно, при n = 1 неравенство справедливо.
Допустим, что оно справедливо при n = k + 1.
Тогда 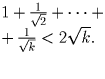 Нужно доказать, что
Нужно доказать, что
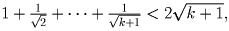 или
или
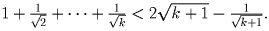 По предположению индукции, достаточно доказать, что
По предположению индукции, достаточно доказать, что
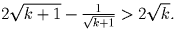 Но это эквивалентно неравенству
Но это эквивалентно неравенству 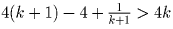 ,
и
,
и 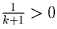 , которое очевидно.
, которое очевидно.Задача 2:
Пусть a1,a2, … ,an, … – произвольная последовательность вещественных чисел. Для натурального n обозначим через fn(x) функцию fn(x) = sin (2nx – an).
а) Докажите, что для любого натурального k найдётся такое число x, что все числа f1(x),f2(x), … ,fk(x) положительны.
б) верно ли аналогичное утверждение, если вместо fn(x) рассматривать функции gn(x) = sin (nx – an)?
(Предложена М.Ф.Прохоровой.)
Решение: а) Зафиксируем натуральное k. Пусть точка x такова, что ни одна из функций fi в ней не равна нулю и fk(x) > 0. Пусть n – наибольший не превосходящий k номер с условием fn(x) < 0. Положим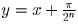 .
Непосредственной подстановкой проверяется, что
fn(y) = – fn(x) > 0, и что fi(y) = fi(x) > 0 при всех
i от n + 1 до k. Повторяя эту операцию столько раз, сколько
необходимо (ясно, что не более k раз)
найдём точку, в которой все числа f1, f2, fk
положительны.
.
Непосредственной подстановкой проверяется, что
fn(y) = – fn(x) > 0, и что fi(y) = fi(x) > 0 при всех
i от n + 1 до k. Повторяя эту операцию столько раз, сколько
необходимо (ясно, что не более k раз)
найдём точку, в которой все числа f1, f2, fk
положительны.б) Нет, неверно. Достаточно рассмотреть функции 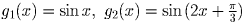 и g3 = sin (3x – π ).
и g3 = sin (3x – π ).
По окружности на равном расстоянии друг от друга расставлено 2n корзин с яблоками, причём число яблок в любых двух соседних корзинах отличается ровно на 1. При каких натуральных n можно гарантировать, что найдутся две диаметрально противоположные корзины, содержащие поровну яблок?
(Предложена С.Э.Нохриным.)
Решение: Заметим, что при переходе к соседней корзине четность числа яблок в ней меняется. Таким образом, если n – нечетное число, то в корзине напротив четность числа яблок будет другой. Значит при нечетном n найти указанную пару нельзя.Пусть теперь n – четное число. Припишем каждой корзине число равное числу яблок, в ней находящихся, минус число яблок, лежащих в противоположной ей корзине. Назовем это число индексом корзины и отметим некоторые их свойства. Первое – индексы любых соседних корзин либо равны, либо отличаются на ± 2. Второе – все индексы являются четными числами, поскольку равны разностям чисел одинаковой четности. Третье – индексы противоположных корзин равны по модулю и противоположны по знаку.
Для решения задачи достаточно показать, что найдется корзина с нулевым индексом. Пусть это не так. Выберем корзину с положительным индексом (это возможно по третьему свойству). Тогда из первого и второго свойств индекс соседней корзины также положителен. Рассуждая аналогично, доказываем, что индексы всех корзин положительны. Однако это противоречит третьему свойству.
Задача 4:Дан выпуклый четырёхгранный угол. Всегда ли найдётся плоскость, сечение которой данного угла является параллелограммом?
((Предложена В.В.Нагребецким.))
Решение: Проведём плоскости через противоположные рёбра угла и отметим на их пересечении произвольную точку O, отличную от вершины. В каждой из плоскостей существует отрезок с концами на рёбрах угла и с серединой в точке O. (Данный отрезок есть основание равнобедренного треугольника, боковые стороны которого лежат на рёбрах угла). По известному признаку концы построенных отрезков являются вершинами искомого параллелограмма.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 11 класс >> 1-й день | Убрать решения |