Задача 1: Найдите сумму всех пятизначных чисел, которые записываются
цифрами 1, 2, 3 и 4.
((Предложена Е.С.Зенковой.))
Решение:
Всего таких чисел 4
5 = 1024, так как в каждом разряде числа
может стоять любая из четырех указанных цифр.
Цифра 1 в первом разряде стоит у ¼ • 1024 = 256 чисел,
цифра 2 – у 256 чисел, цифра 3 – у 256 чисел и
цифра 4 – у 256 чисел.
Следовательно, сумма цифр первого разряда – (1 + 2 + 3 + 4) • 256 = 2560.
Аналогично, вычисляется сумма цифр второго, третьего, четвертого и
пятого разрядов. Искомая сумма равна 2560 • (1 + 10 + 100 + 1000 + 10000) = 11111 • 2560.
Задача 2: Имеется 16 камней, веса которых попарно различны. Как
с помощью чашечных весов (без гирь) за 18 взвешиваний
выбрать из них два наиболее тяжёлых?
((Взята из сборника ``Ленинградские математические кружки".))
Решение:
Пронумеруем камни.
Разобьём 16 камней на 8 пар и попарно взвешиваем камни,
отбирая из любой пары тяжелый. Оставшиеся 8 камней разбиваем на 4 пары
и проделываем аналогичный отбор. И так далее. Тогда самый тяжёлый
камень мы определим за 8 + 4 + 2 + 1 = 15 взвешиваний.
Второй по тяжести камень находится среди тех четырех камней,
с которыми во время вышеописанной процедуры отбора взвешивался
самый тяжёлый камень. Так как все камни были пронумерованы,
эти четыре камня легко выявляются, и самый тяжёлый из них определяется
за 2 + 1 = 3 взвешивания.
Задача 3: Пусть ABC – произвольный треугольник и
O – точка внутри треугольника. Доказать, что 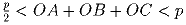 ,
где p – периметр треугольника.
,
где p – периметр треугольника.
Решение:
Для любого треугольника верно:
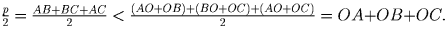
Левое неравенство доказано. Пусть M – точка пересечения прямых
AO и BC. Тогда AO + OB < AM + MB < AC + CM + MB = AC + CB. Аналогично, AO + OC < AB + BC
и BO + OC < AB + AC. Для завершения доказательства остаётся сложить
три полученных неравенства.


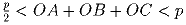 ,
где p – периметр треугольника.
,
где p – периметр треугольника.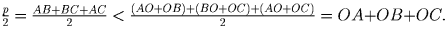 Левое неравенство доказано. Пусть M – точка пересечения прямых
AO и BC. Тогда AO + OB < AM + MB < AC + CM + MB = AC + CB. Аналогично, AO + OC < AB + BC
и BO + OC < AB + AC. Для завершения доказательства остаётся сложить
три полученных неравенства.
Левое неравенство доказано. Пусть M – точка пересечения прямых
AO и BC. Тогда AO + OB < AM + MB < AC + CM + MB = AC + CB. Аналогично, AO + OC < AB + BC
и BO + OC < AB + AC. Для завершения доказательства остаётся сложить
три полученных неравенства.